Somos's Quadratic Recurrence Constant

Somos's quadratic recurrence constant is defined via the sequence

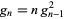(1)

with 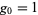. This has closed-form solution

(2)

where 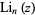 is a polylogarithm,  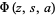is a Lerch transcendent. The first few terms are 1, 2, 12, 576, 1658880, 16511297126400, ... (OEIS A052129). The terms of this sequence have asymptotic growth as

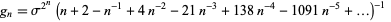(3)

(OEIS A116603; Finch 2003, p. 446, 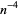 term corrected), where  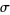is known as Somos's quadratic recurrence constant. Here, the generating functio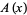n  in 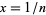 satisfies the functional equation

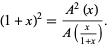(4)

Expressions for 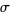 include

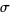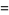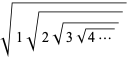			(5)
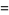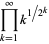			(6)
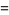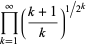			(7)
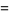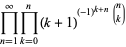			(8)
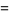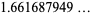			(9)

(OEIS A112302; Ramanujan 2000, p. 348; Finch 2003, p. 446; Guillera and Sondow 2005).

Expressions for 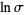 include

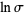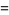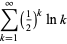			(10)
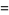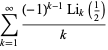			(11)
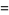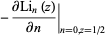			(12)
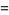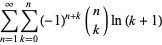			(13)
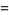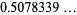			(14)

(OEIS A114124; Finch 2003, p. 446; Guillera and Sondow 2005; J. Borwein, pers. comm., Feb. 6, 2005), where 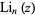 is a polylogarithm.

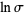 is also given by the unit square integral

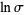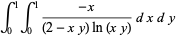			(15)
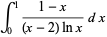			(16)

(Guillera and Sondow 2005).

Ramanujan (1911; 2000, p. 323) proposed finding the nested radical expression

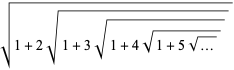(17)

which converges to 3. Vijayaraghavan (in Ramanujan 2000, p. 348) gives the justification of his process both in general, and in the particular example of .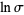

REFERENCES:

Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.

Guillera, J. and Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005 https://arxiv.org/abs/math.NT/0506319.

Ramanujan, S. Question No. 298. J. Indian Math. Soc. 1911.

Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., 2000.

Sloane, N. J. A. Sequences A052129, A112302, A114124, and A116603 in "The On-Line Encyclopedia of Integer Sequences."

Somos, M. "Several Constants Related to Quadratic Recurrences." Unpublished note. 1999.