Mertens Theorem

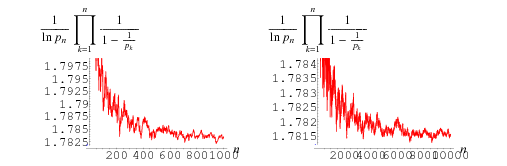
Consider the Euler product

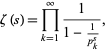(1)

where 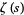 is the Riemann zeta function and  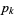is the 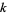th prime. 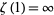, but taking the finite product up to 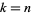, premultiplying by a factor 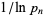, and letting  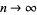gives

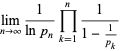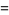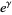			(2)
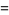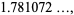			(3)

where 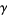 is the Euler-Mascheroni constant (Havil 2003, p. 173). This amazing result is known as the Mertens theorem.

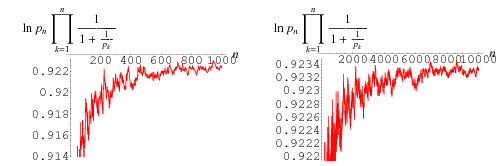
At least for 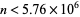, the sequence of finite products approaches  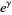strictly from above (Rosser and Schoenfeld 1962). However, it is highly likely that the finite product is less than its limiting value for infinitely many values of 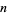, which is usually the case for any such inequality due to the presence of zeros of  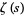on the critical line . An example is Littlewood's famous proof that the sense of the inequality 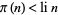, where  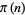is the prime counting function and  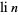is the logarithmic integral, reverses infinitely often. While Rosser and Schoenfeld (1962) suggest that "perhaps one can extend [this] result to show that [the Mertens inequality] fails for large ; we have not investigated the matter," a full proof of the reversal of the inequality for terms in the Mertens theorem does not seem to appear anywhere in the published literature.

A closely related result is obtained by noting that

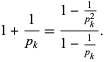(4)

Considering the variation of (3) with the 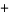 sign changed to a  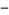sign and the  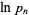moved from the denominator to the numerator then gives

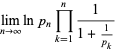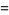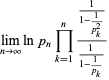			(5)
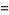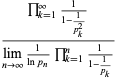			(6)
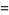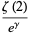			(7)
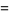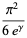			(8)
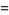			(9)

The sequence of finite products approaches its limiting value strictly from below for the same range as for the Mertens theorem, since this inequality from below is a consequence of the Mertens inequality from above.

Edwards (2001, pp. 5-6) remarks, "For the first 30 years after Riemann's [1859] paper was published, there was virtually no progress in the field [of prime number asymptotics]," adding as a footnote, "A major exception to this statement was Mertens's Theorem of 1874...." (The celebrated prime number theorem was not proved until 1896.)

REFERENCES:

Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford University Press, p. 351, 1979.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Mertens, F. "Ein Beitrag zur analytischen Zahlentheorie." J. reine angew. Math. 78, 46-62, 1874.

Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 66-67, 1994.

Rosser, J. B. and Schoenfeld, L. "Approximate Formulas for Some Functions of Prime Numbers." Ill. J. Math. 6, 64-94, 1962.