


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-11-2019
Date: 24-9-2020
Date: 13-8-2020
|
Sphere line picking is the selection of pairs of points corresponding to vertices of a line segment with endpoints on the surface of a sphere. 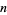 random line segments can be picked on a unit sphere in the Wolfram Language using the function RandomPoint[Sphere[],
random line segments can be picked on a unit sphere in the Wolfram Language using the function RandomPoint[Sphere[],  n, 2
n, 2 ].
].
Pick two points at random on a unit sphere. The first one can be placed at the north pole, i.e., assigned the coordinate (0, 0, 1), without loss of generality. The second point is then chosen at random using sphere point picking, and so can be assigned coordinates
 |
 |
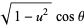 |
(1) |
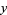 |
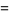 |
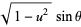 |
(2) |
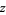 |
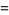 |
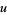 |
(3) |
with ![u in [-1,1]](http://mathworld.wolfram.com/images/equations/SphereLinePicking/Inline13.gif) and
and 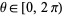 . The distance
. The distance 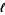 between first and second points is then
between first and second points is then
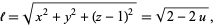 |
(4) |
and solving for 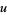 gives
gives
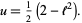 |
(5) |
Now the probability function 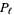 for distance is then given by
for distance is then given by
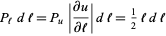 |
(6) |
(Solomon 1978, p. 163), since 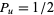 and
and 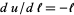 . Here,
. Here, ![l in [0,2]](http://mathworld.wolfram.com/images/equations/SphereLinePicking/Inline20.gif) .
.

Therefore, somewhat surprisingly, large distances are the most common, contrary to most people's intuition. A plot of 15 random lines is shown above. The raw moments are
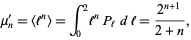 |
(7) |
giving the first few as
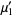 |
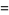 |
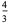 |
(8) |
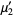 |
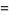 |
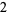 |
(9) |
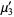 |
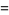 |
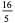 |
(10) |
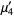 |
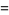 |
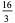 |
(11) |
(OEIS A084623 and A000265). Values of 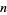 for which
for which 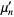 are integers are therefore
are integers are therefore 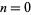 , 2, 6, 14, 30, 62, 126, 254, 510, 1022, ... (OEIS A000918), which are precisely the values
, 2, 6, 14, 30, 62, 126, 254, 510, 1022, ... (OEIS A000918), which are precisely the values 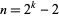 .
.
The central moments are
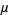 |
 |
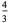 |
(12) |
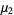 |
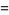 |
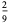 |
(13) |
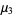 |
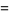 |
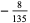 |
(14) |
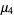 |
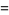 |
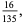 |
(15) |
so the variance, skewness and kurtosis excess are
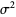 |
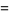 |
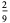 |
(16) |
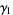 |
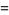 |
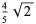 |
(17) |
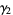 |
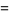 |
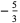 |
(18) |
(Solomon 1978, p. 163).
REFERENCES:
Sloane, N. J. A. Sequences A000265/M2222, A000918/M1599, and A084623 in "The On-Line Encyclopedia of Integer Sequences."
Solomon, H. Geometric Probability. Philadelphia, PA: SIAM, 1978.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|