


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-12-2020
Date: 24-9-2020
Date: 13-11-2019
|
The average distance between two points chosen at random inside a unit cube (the 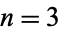 case of hypercube line picking), sometimes known as the Robbins constant, is
case of hypercube line picking), sometimes known as the Robbins constant, is
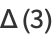 |
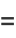 |
![1/(105)[4+17sqrt(2)-6sqrt(3)+21ln(1+sqrt(2))+42ln(2+sqrt(3))-7pi]](http://mathworld.wolfram.com/images/equations/CubeLinePicking/Inline4.gif) |
(1) |
 |
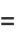 |
![1/(105)[4+17sqrt(2)-6sqrt(3)+21sinh^(-1)1+42ln(2+sqrt(3))-7pi]](http://mathworld.wolfram.com/images/equations/CubeLinePicking/Inline7.gif) |
(2) |
 |
 |
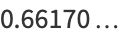 |
(3) |
(OEIS A073012; Robbins 1978, Le Lionnais 1983).
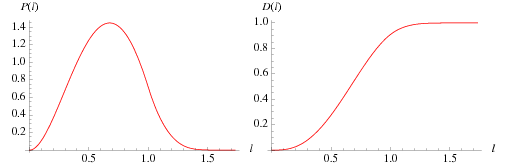
The probability function as a function of line length, illustrated above, was found in (nearly) closed form by Mathai et al. (1999). After simplifying, correcting typos, and completing the integrals, gives the closed form
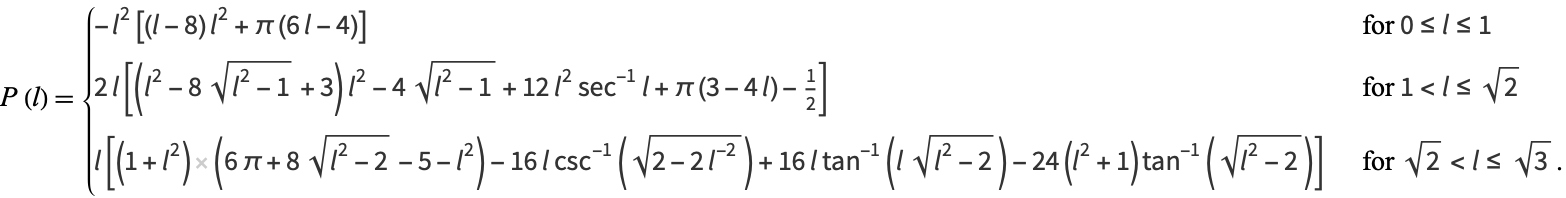 |
(4) |
The first even raw moments 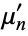 for
for 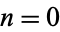 , 2, ... are 1, 1/2, 11/30, 211/630, 187/525, 3524083/6306300, ... (OEIS A160693 and A160694).
, 2, ... are 1, 1/2, 11/30, 211/630, 187/525, 3524083/6306300, ... (OEIS A160693 and A160694).
Pick 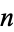 points on a cube, and space them as far apart as possible. The best value known for the minimum straight line distance between any two points is given in the following table.
points on a cube, and space them as far apart as possible. The best value known for the minimum straight line distance between any two points is given in the following table.
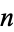 |
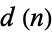 |
| 5 | 1.1180339887498 |
| 6 | 1.0606601482100 |
| 7 | 1 |
| 8 | 1 |
| 9 | 0.86602540378463 |
| 10 | 0.74999998333331 |
| 11 | 0.70961617562351 |
| 12 | 0.70710678118660 |
| 13 | 0.70710678118660 |
| 14 | 0.70710678118660 |
| 15 | 0.625 |
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006b.
Bolis, T. S. Solution to Problem E2629. "Average Distance between Two Points in a Box." Amer. Math. Monthly 85, 277-278, 1978.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Finch, S. R. "Geometric Probability Constants." §8.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 479-484, 2003.
Ghosh, B. "Random Distances within a Rectangle and between Two Rectangles." Bull. Calcutta Math. Soc. 43, 17-24, 1951.
Holshouser, A. L.; King, L. R.; and Klein, B. G. Solution to Problem E3217, "Minimum Average Distance between Points in a Rectangle." Amer. Math. Monthly 96, 64-65, 1989.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 30, 1983.
Mathai, A. M.; Moschopoulos, P.; and Pederzoli, G. "Distance between Random Points in a Cube." J. Statistica 59, 61-81, 1999.
Robbins, D. "Average Distance between Two Points in a Box." Amer. Math. Monthly 85, 278, 1978.
Santaló, L. A. Integral Geometry and Geometric Probability. Reading, MA: Addison-Wesley, 1976.
Schroeppel, R. (results due to R. H. Hardin and N. J. A. Sloane) "points in a cube." math-fun@cs.arizona.edu posting, May 30, 1996.
Sloane, N. J. A. Sequences A073012, A160693, and A160694 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|