


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-10-2020
Date: 24-9-2020
Date: 23-11-2020
|
Let 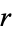 and
and 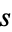 be positive integers which are relatively prime and let
be positive integers which are relatively prime and let 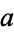 and
and 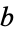 be any two integers. Then there is an integer
be any two integers. Then there is an integer 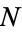 such that
such that
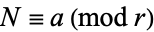 |
(1) |
and
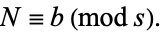 |
(2) |
Moreover, 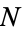 is uniquely determined modulo
is uniquely determined modulo 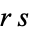 . An equivalent statement is that if
. An equivalent statement is that if 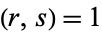 , then every pair of residue classes modulo
, then every pair of residue classes modulo 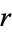 and
and 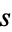 corresponds to a simple residue class modulo
corresponds to a simple residue class modulo 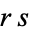 .
.
The Chinese remainder theorem is implemented in the Wolfram Language as ChineseRemainder[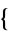 a1, a2, ...
a1, a2, ...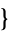
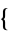 m1, m2, ...
m1, m2, ... ]. The Chinese remainder theorem is also implemented indirectly using Reduce in with a domain specification of Integers.
]. The Chinese remainder theorem is also implemented indirectly using Reduce in with a domain specification of Integers.
The theorem can also be generalized as follows. Given a set of simultaneous congruences
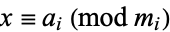 |
(3) |
for 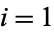 , ...,
, ..., 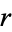 and for which the
and for which the 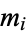 are pairwise relatively prime, the solution of the set of congruences is
are pairwise relatively prime, the solution of the set of congruences is
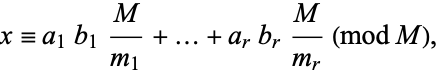 |
(4) |
where
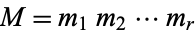 |
(5) |
and the 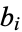 are determined from
are determined from
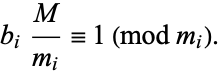 |
(6) |
REFERENCES:
Flannery, S. and Flannery, D. In Code: A Mathematical Journey. London: Profile Books, pp. 123-125, 2000.
Ireland, K. and Rosen, M. "The Chinese Remainder Theorem." §3.4 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 34-38, 1990.
Séroul, R. "The Chinese Remainder Theorem." §2.6 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 12-14, 2000.
Uspensky, J. V. and Heaslet, M. A. Elementary Number Theory. New York: McGraw-Hill, pp. 189-191, 1939.
Wagon, S. "The Chinese Remainder Theorem." §8.4 in Mathematica in Action. New York: W. H. Freeman, pp. 260-263, 1991.



|
|
|
|
إدارة الغذاء والدواء الأميركية تقرّ عقارا جديدا للألزهايمر
|
|
|
|
|
|
|
شراء وقود الطائرات المستدام.. "الدفع" من جيب المسافر
|
|
|
|
|
|
|
إيذانًا بحلول شهر المحرّم الحرام 1446هـ العتبة العبّاسيّة تنظّم مراسم استبدال راية قبّة مرقد أبي الفضل العبّاس (عليه السّلام) من الحمراء إلى السّوداء
|
|
|