Egyptian Number

A number 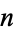 is called an Egyptian number if it is the sum of the denominators in some unit fraction representation of a positive whole number not consisting entirely of 1s. For example,

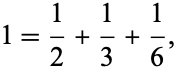so 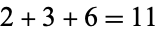 is an Egyptian number. The numbers that are not Egyptian are 2, 3, 5, 6, 7, 8, 12, 13, 14, 15, 19, 21, and 23 (OEIS A028229; Konhauser et al. 1996, p. 147).

If 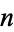 is the sum of denominators of a unit fraction representation composed of distinct denominators which are not all 1s, then it is called a strictly Egyptian number. For example, by virtue of

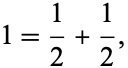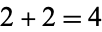 is Egyptian, but it is not strictly Egyptian. Graham (1963) proved that every number  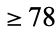is strictly Egyptian. Numbers that are strictly Egyptian are 11, 24, 30, 31, 32, 37, 38, 43, ... (OEIS A052428), and those which are not are 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, ... (OEIS A051882).

REFERENCES:

Graham, R. L. "A Theorem on Partitions." J. Austral. Math. Soc. 3, 435-441, 1963.

Konhauser, J. D. E.; Vellman, D.; and Wagon, S. Which Way Did the Bicycle Go and Other Intriguing Mathematical Mysteries. Washington, DC: Amer. Math. Soc., 1996.

Sloane, N. J. A. Sequences A028229, A051882, and A052428 in "The On-Line Encyclopedia of Integer Sequences."