


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-6-2019
Date: 3-9-2019
Date: 22-4-2019
|
The first solution to Lamé's differential equation, denoted 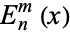 for
for 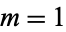 , ...,
, ..., 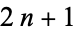 . They are also called Lamé functions. The product of two ellipsoidal harmonics of the first kind is a spherical harmonic. Whittaker and Watson (1990, pp. 536-537) write
. They are also called Lamé functions. The product of two ellipsoidal harmonics of the first kind is a spherical harmonic. Whittaker and Watson (1990, pp. 536-537) write
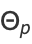 |
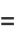 |
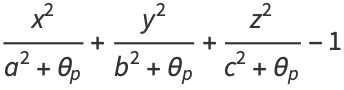 |
(1) |
 |
 |
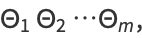 |
(2) |
and give various types of ellipsoidal harmonics and their highest degree terms as
1. 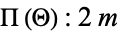
2. 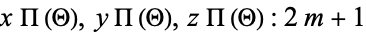
3. 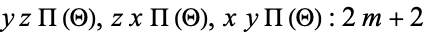
4. 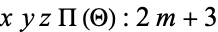 .
.
A Lamé function of degree 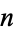 may be expressed as
may be expressed as
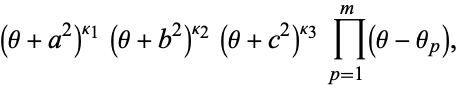 |
(3) |
where 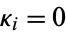 or 1/2,
or 1/2, 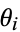 are real and unequal to each other and to
are real and unequal to each other and to 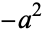 ,
, 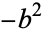 , and
, and 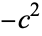 , and
, and
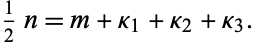 |
(4) |
Byerly (1959) uses the recurrence relations to explicitly compute some ellipsoidal harmonics, which he denoted by 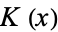 ,
, 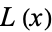 ,
, 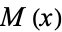 , and
, and 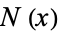 ,
,
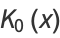 |
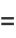 |
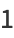 |
(5) |
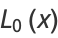 |
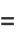 |
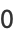 |
(6) |
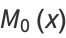 |
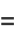 |
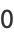 |
(7) |
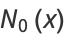 |
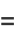 |
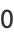 |
(8) |
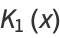 |
 |
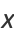 |
(9) |
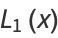 |
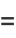 |
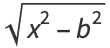 |
(10) |
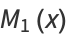 |
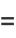 |
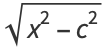 |
(11) |
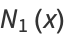 |
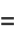 |
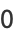 |
(12) |
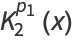 |
 |
![x^2-1/3[b^2+c^2-sqrt((b^2+c^2)^2-3b^2c^2)]](http://mathworld.wolfram.com/images/equations/EllipsoidalHarmonicoftheFirstKind/Inline50.gif) |
(13) |
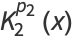 |
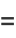 |
![x^2-1/3[b^2+c^2+sqrt((b^2+c^2)^2-3b^2c^2)]](http://mathworld.wolfram.com/images/equations/EllipsoidalHarmonicoftheFirstKind/Inline53.gif) |
(14) |
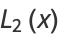 |
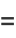 |
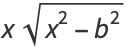 |
(15) |
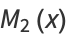 |
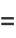 |
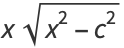 |
(16) |
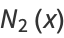 |
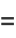 |
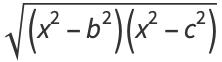 |
(17) |
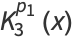 |
 |
![x^3-1/5x[2(b^2+c^2)-sqrt(4(b^2+c^2)^2-15b^2c^2)]](http://mathworld.wolfram.com/images/equations/EllipsoidalHarmonicoftheFirstKind/Inline65.gif) |
(18) |
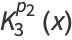 |
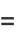 |
![x^3-1/5x[2(b^2+c^2)+sqrt(4(b^2+c^2)^2-15b^2c^2)]](http://mathworld.wolfram.com/images/equations/EllipsoidalHarmonicoftheFirstKind/Inline68.gif) |
(19) |
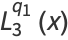 |
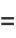 |
![sqrt(x^2-b^2)[x^2-1/5(b^2+2c^2-sqrt((b^2+2c^2)^2-5b^2c^2))]](http://mathworld.wolfram.com/images/equations/EllipsoidalHarmonicoftheFirstKind/Inline71.gif) |
(20) |
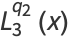 |
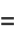 |
![sqrt(x^2-b^2)[x^2-1/5(b^2+2c^2+sqrt((b^2+2c^2)^2-5b^2c^2))]](http://mathworld.wolfram.com/images/equations/EllipsoidalHarmonicoftheFirstKind/Inline74.gif) |
(21) |
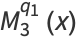 |
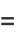 |
![sqrt(x^2-c^2)[x^2-1/5(2b^2+c^2-sqrt((2b^2+c^2)^2-5b^2c^2))]](http://mathworld.wolfram.com/images/equations/EllipsoidalHarmonicoftheFirstKind/Inline77.gif) |
(22) |
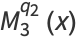 |
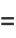 |
![sqrt(x^2-c^2)[x^2-1/5(2b^2+c^2+sqrt((2b^2+c^2)^2-5b^2c^2))]](http://mathworld.wolfram.com/images/equations/EllipsoidalHarmonicoftheFirstKind/Inline80.gif) |
(23) |
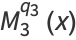 |
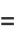 |
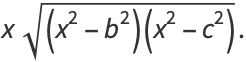 |
(24) |
REFERENCES:
Byerly, W. E. "Laplace's Equation in Curvilinear Coördinates. Ellipsoidal Harmonics." Ch. 8 in An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, pp. 251-266, 1959.
Humbert, P. Fonctions de Lamé et Fonctions de Mathieu. Paris: Gauthier-Villars, 1926.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|