المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Ramanujan Log-Trigonometric Integrals |
 1348
 12:48 صباحاً
date: 4-9-2019 |
Author : Oloa, O 
Book or Source : "Two Conjectures on Ramanujan Log-trigonometric Integrals." Unpublished manuscript. January 2010. 
Page and Part : ...|
Read More
Date: 3-9-2019
2013
Date: 20-6-2019
1268
Date: 17-6-2019
2598
|
Oloa (2010, pers. comm., Jan. 20, 2010) has considered the following integrals containing nested radicals of 1/2 plus terms in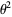 
and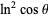 
:
 |
 |
 |
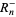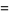(1) |
 |
 |
 |
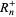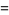(2) |
which he terms Ramanujan log-trigonometric integrals because they involve terms like Ramanujan's nested radicals of 1/2.
The special case
 |
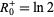(3) |
was known to Euler.
Amazingly, the general integrals have closed forms
 |
 |
 |
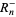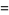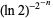(4) |
 |
 |
 |
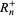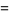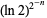(5) |
for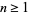 
.
REFERENCES:
Oloa, O. "Two Conjectures on Ramanujan Log-trigonometric Integrals." Unpublished manuscript. January 2010.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
