


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-5-2018
Date: 7-8-2019
Date: 8-9-2019
|
Macdonald's plane partition conjecture proposes a formula for the number of cyclically symmetric plane partitions (CSPPs) of a given integer whose Ferrers diagrams fit inside an 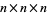 box. Macdonald gave a product representation for the power series whose coefficients
box. Macdonald gave a product representation for the power series whose coefficients 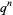 were the number of such partitions of
were the number of such partitions of 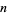 .
.
Let 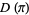 be the set of all integer points
be the set of all integer points 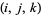 in the first octant such that a plane partition
in the first octant such that a plane partition 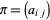 is defined and
is defined and 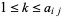 . Then
. Then 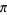 is said to be cyclically symmetric if
is said to be cyclically symmetric if 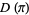 is invariant under the mapping
is invariant under the mapping 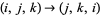 . Let
. Let 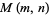 be the number of cyclically symmetric partitions of
be the number of cyclically symmetric partitions of 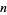 such that none of
such that none of 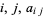 exceed
exceed 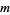 . Let
. Let 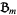 be the box containing all integer points
be the box containing all integer points 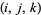 such that
such that 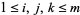 , then
, then 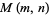 is the number of cyclically symmetric plane partitions of
is the number of cyclically symmetric plane partitions of 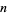 such that
such that 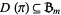 . Now, let
. Now, let 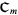 be the set of all the orbits in
be the set of all the orbits in 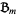 . Finally, for each point
. Finally, for each point 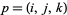 in
in 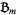 , let its height
, let its height
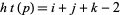 |
(1) |
and for each 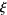 in
in 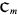 , let
, let 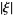 be the number of points in
be the number of points in 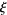 (either 1 or 3) and write
(either 1 or 3) and write
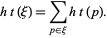 |
(2) |
Then Macdonald conjectured that
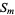 |
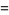 |
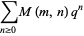 |
(3) |
 |
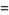 |
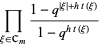 |
(4) |
 |
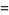 |
![product_(i=1)^(m)[(1-q^(3i-1))/(1-q^(3i-2))product_(j=i)^(m)(1-q^(3(m+i+j-1)))/(1-q^(3(2i+j-1)))],](http://mathworld.wolfram.com/images/equations/MacdonaldsPlanePartitionConjecture/Inline37.gif) |
(5) |
(Mills et al. 1982, Macdonald 1995), where the latter form is due to Andrews (1979).
The first few polynomials are
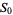 |
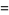 |
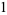 |
(6) |
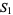 |
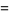 |
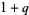 |
(7) |
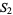 |
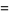 |
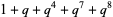 |
(8) |
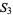 |
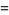 |
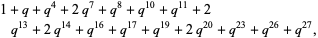 |
(9) |
which converge to the polynomial with coefficients 1, 1, 0, 0, 1, 0, 0, 2, 1, 0, 2, 1, 0, 4, 3, 0, 5, 4, 0, 8, 8, ... (OEIS A096419).
Andrews (1979) proved the 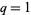 case, giving the total number of CSPPs fitting inside an
case, giving the total number of CSPPs fitting inside an 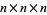 box. The general case was proved by Mills et al. (1982).
box. The general case was proved by Mills et al. (1982).
REFERENCES:
Andrews, G. E. "Plane Partitions (III): The Weak Macdonald Conjecture." Invent. Math. 53, 193-225, 1979.
Andrews, G. E. "Macdonald's Conjecture and Descending Plane Partitions." In Combinatorics, Representation Theory and Statistical Methods in Groups (Ed. T. V. Narayana, R. M. Mathsen, and J. G. Williams). New York: Dekker, pp. 91-106, 1980.
Bressoud, D. Proofs and Confirmations: The Story of the Alternating Sign Matrix Conjecture. Cambridge, England: Cambridge University Press, 1999.
Bressoud, D. and Propp, J. "How the Alternating Sign Matrix Conjecture was Solved." Not. Amer. Math. Soc. 46, 637-646.
Macdonald, I. G. "Some conjectures for Root Systems." SIAM J. Math. Anal. 13, 988-1007, 1982.
Macdonald, I. G. Symmetric Functions and Hall Polynomials, 2nd ed. Oxford, England: Oxford University Press, 1995.
Mills, W. H.; Robbins, D. P.; and Rumsey, H. Jr. "Proof of the Macdonald Conjecture." Invent. Math. 66, 73-87, 1982.
Morris, W. G. Constant Term Identities for Finite and Affine Root Systems: Conjectures and Theorems. Ph.D. thesis. Madison, WI: University of Wisconsin, 1982.
Sloane, N. J. A. Sequence A096419 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|