

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Sinc Function
المؤلف:
Baillie, R.
المصدر:
"Advanced Problem 6241." Amer. Math. Monthly 85
الجزء والصفحة:
...
25-7-2019
6316
Sinc Function
 |
The sinc function 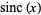 , also called the "sampling function," is a function that arises frequently in signal processing and the theory of Fourier transforms. The full name of the function is "sine cardinal," but it is commonly referred to by its abbreviation, "sinc." There are two definitions in common use. The one adopted in this work defines
, also called the "sampling function," is a function that arises frequently in signal processing and the theory of Fourier transforms. The full name of the function is "sine cardinal," but it is commonly referred to by its abbreviation, "sinc." There are two definitions in common use. The one adopted in this work defines
|
(1) |
where 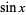 is the sine function, plotted above.
is the sine function, plotted above.
This has the normalization
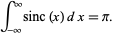 |
(2) |
This function is implemented in the Wolfram Language as Sinc[x].
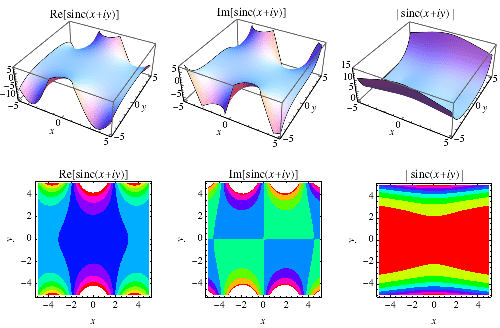 |
When extended into the complex plane, 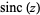 is illustrated above.
is illustrated above.
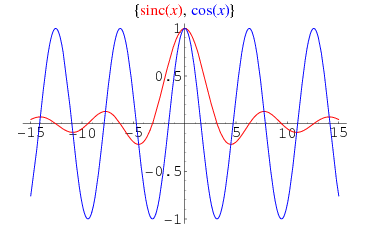
An interesting property of 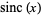 is that the set of local extrema of
is that the set of local extrema of 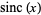 corresponds to its intersections with the cosine function
corresponds to its intersections with the cosine function 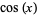 , as illustrated above.
, as illustrated above.
The derivative is given by
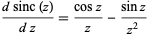 |
(3) |
and the indefinite integral by
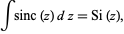 |
(4) |
where 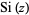 is the sine integral.
is the sine integral.
Woodward (1953), McNamee et al. (1971), and Bracewell (1999, p. 62) adopt the alternative definition
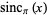 |
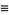 |
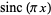 |
(5) |
 |
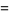 |
(6) |
The latter definition is sometimes more convenient as a result of its simple normalization,
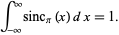 |
(7) |
That variant also satisfies the sum
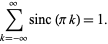 |
(8) |
In addition, the binomial coefficient satisfies
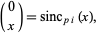 |
(9) |
which is essentially a restatement of the reflection relation
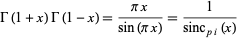 |
(10) |
of the gamma function (M. Somos, pers. comm., Oct. 26, 2006.)
The sinc function is closely related to the spherical Bessel function of the first kind 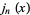 and, in particular,
and, in particular,
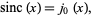 |
(11) |
and is given in terms of the Meijer G-function as
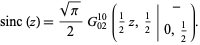 |
(12) |
Let 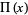 be the rectangle function, then the Fourier transform of
be the rectangle function, then the Fourier transform of 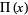 is the sinc function
is the sinc function
=sinc(pik).](http://mathworld.wolfram.com/images/equations/SincFunction/NumberedEquation11.gif) |
(13) |
The sinc function therefore frequently arises in physical applications such as Fourier transform spectroscopy as the so-called instrument function, which gives the instrumental response to a delta function input. Removing the instrument functions from the final spectrum requires use of some sort of deconvolution algorithm.
The sinc function can be written as a complex integral by noting that, for 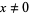 ,
,
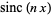 |
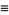 |
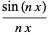 |
(14) |
 |
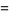 |
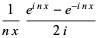 |
(15) |
 |
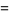 |
![1/(2inx)[e^(itx)]_(-n)^n](http://mathworld.wolfram.com/images/equations/SincFunction/Inline26.gif) |
(16) |
 |
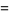 |
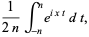 |
(17) |
and that 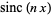 and the integral both equal 1 for
and the integral both equal 1 for 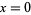 .
.
The sinc function can also be written as the infinite product
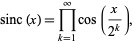 |
(18) |
a result discovered in 1593 by Francois Viète (Kac 1959, Morrison 1995) and sometimes known as Euler's formula (Prudnikov et al. 1986, p. 757; Gearhart and Shulz 1990). It is also given by
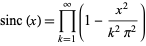 |
(19) |
(Gearhart and Shulz 1990) and
![sinc(x)=product_(k=1)^infty[1-4/3sin^2(x/(3^k))]](http://mathworld.wolfram.com/images/equations/SincFunction/NumberedEquation14.gif) |
(20) |
(Prudnikov et al. 1986, p. 757).
Another product is given by
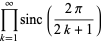 |
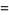 |
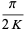 |
(21) |
 |
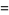 |
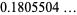 |
(22) |
(OEIS A118253; Prudnikov et al. 1986, p. 757), where 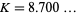 is the constant from polygon circumscribing.
is the constant from polygon circumscribing.
Sums of powers of 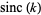 over the positive integers include
over the positive integers include
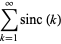 |
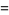 |
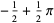 |
(23) |
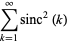 |
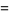 |
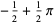 |
(24) |
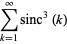 |
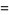 |
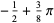 |
(25) |
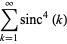 |
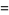 |
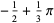 |
(26) |
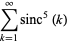 |
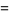 |
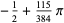 |
(27) |
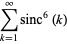 |
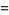 |
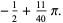 |
(28) |
The remarkable fact that the sums of 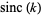 and
and 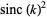 are equal appears to have first been published in Baillie (1978). Amazingly, the pattern of these sums being equal to
are equal appears to have first been published in Baillie (1978). Amazingly, the pattern of these sums being equal to 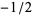 plus a rational multiple of
plus a rational multiple of 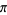 breaks down for the power
breaks down for the power 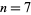 , where the sum equals
, where the sum equals
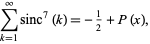 |
(29) |
where
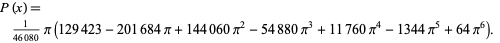 |
(30) |
The sinc function satisfies the identity
![int_(-infty)^inftysinc[pi(x-y)]sinc(piy)dy=sinc(pix).](http://mathworld.wolfram.com/images/equations/SincFunction/NumberedEquation17.gif) |
(31) |
Definite integrals involving the sinc function include
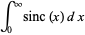 |
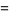 |
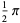 |
(32) |
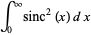 |
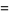 |
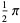 |
(33) |
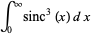 |
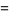 |
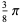 |
(34) |
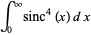 |
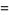 |
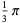 |
(35) |
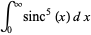 |
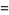 |
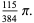 |
(36) |
After dividing out the constant factor of 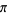 , the values are again 1/2, 1/2, 3/8, 1/3, 115/384, 11/40, 5887/23040, 151/630, 259723/1146880, ... (OEIS A049330 and A049331; Grimsey 1945, Medhurst and Roberts 1965). These are all special cases of the amazing general result
, the values are again 1/2, 1/2, 3/8, 1/3, 115/384, 11/40, 5887/23040, 151/630, 259723/1146880, ... (OEIS A049330 and A049331; Grimsey 1945, Medhurst and Roberts 1965). These are all special cases of the amazing general result
![int_0^infty(sin^ax)/(x^b)dx=(pi^(1-c)(-1)^(|_(a-b)/2_|))/(2^(a-c)(b-1)!)sum_(k=0)^(|_a/2_|-c)(-1)^k(a; k)(a-2k)^(b-1)[ln(a-2k)]^c,](http://mathworld.wolfram.com/images/equations/SincFunction/NumberedEquation18.gif) |
(37) |
where 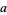 and
and 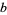 are positive integers such that
are positive integers such that 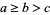 ,
, 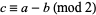 ,
, 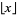 is the floor function, and
is the floor function, and 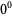 is taken to be equal to 1 (Kogan). This spectacular formula simplifies in the special case when
is taken to be equal to 1 (Kogan). This spectacular formula simplifies in the special case when 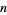 is a positive even integer to
is a positive even integer to
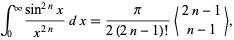 |
(38) |
where 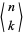 is an Eulerian number (Kogan). The solution of the integral can also be written in terms of the recurrence relation for the coefficients
is an Eulerian number (Kogan). The solution of the integral can also be written in terms of the recurrence relation for the coefficients
|
(39) |
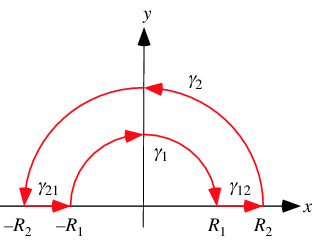
The half-infinite integral of 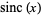 can be derived using contour integration. In the above figure, consider the path
can be derived using contour integration. In the above figure, consider the path 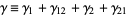 . Now write
. Now write 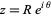 . On an arc,
. On an arc, 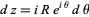 and on the x-axis,
and on the x-axis, 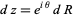 . Write
. Write
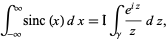 |
(40) |
where 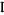 denotes the imaginary part. Now define
denotes the imaginary part. Now define
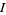 |
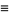 |
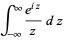 |
(41) |
 |
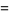 |
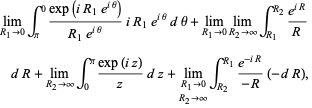 |
(42) |
where the second and fourth terms use the identities 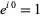 and
and 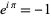 . Simplifying,
. Simplifying,
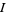 |
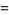 |
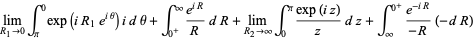 |
(43) |
 |
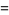 |
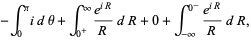 |
(44) |
where the third term vanishes by Jordan's lemma. Performing the integration of the first term and combining the others yield
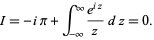 |
(45) |
Rearranging gives
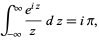 |
(46) |
so
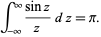 |
(47) |
The same result is arrived at using the method of complex residues by noting
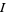 |
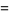 |
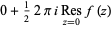 |
(48) |
 |
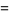 |
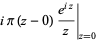 |
(49) |
 |
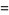 |
![ipi[e^(iz)]_(z=0)](http://mathworld.wolfram.com/images/equations/SincFunction/Inline115.gif) |
(50) |
 |
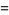 |
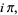 |
(51) |
so
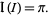 |
(52) |
Since the integrand is symmetric, we therefore have
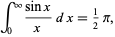 |
(53) |
giving the sine integral evaluated at 0 as
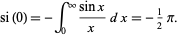 |
(54) |
REFERENCES:
Baillie, R. "Advanced Problem 6241." Amer. Math. Monthly 85, 828, 1978.
Baillie, R.; Henrici, P.; and Johnsonbaugh, R. "Solution to Advanced Problem 6241." Amer. Math. Monthly 87, 496-498, 1980.
Bracewell, R. "The Filtering or Interpolating Function, 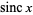 ." In The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, pp. 62-64, 1999.
." In The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, pp. 62-64, 1999.
Brown, J. W. and Churchill, R. V. Fourier Series and Boundary Value Problems, 5th ed. New York: McGraw-Hill, 1993.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.
Gearhart, W. B. and Schulz, H. S. "The Function 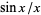 ." College Math. J. 21, 90-99, 1990. http://www.maa.org/pubs/Calc_articles/ma003.pdf.
." College Math. J. 21, 90-99, 1990. http://www.maa.org/pubs/Calc_articles/ma003.pdf.
Grimsey, A. H. R. "On the Accumulation of Chance Effects and the Gaussian Frequency Distribution." Phil. Mag. 36, 294-295, 1945.
Higgins, J. R. "Five Short Stories About the Cardinal Series." Bull. Amer. Math. Soc. 12, 45-89, 1985.
Kac, M. Statistical Independence in Probability, Analysis and Number Theory. Washington, DC: Math. Assoc. Amer., 1959.
McNamee, J.; Stenger, F.; and Whitney, E. L. "Whittaker's Cardinal Function in Retrospect." Math. Comput. 25, 141-154, 1971.
Medhurst, R. G. and Roberts, J. H. "Evaluation of the Integral 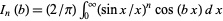 ." Math. Comput. 19, 113-117, 1965.
." Math. Comput. 19, 113-117, 1965.
Morrison, K. E. "Cosine Products, Fourier Transforms, and Random Sums." Amer. Math. Monthly 102, 716-724, 1995.
Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. Integrals and Series, Vol. 1: Elementary Functions. New York: Gordon & Breach, 1986.
Sloane, N. J. A. Sequences A049330, A049331, and A118253 in "The On-Line Encyclopedia of Integer Sequences."
Stenger, F. Numerical Methods Based on Sinc and Analytic Functions. New York: Springer-Verlag, 1993.
Woodward, P. M. Probability and Information Theory with Applications to Radar. New York: McGraw-Hill, 1953.
Zimmermann, P. "Int(sin(x)^k/x^k,x=0..infinity)." math-fun@cs.arizona.edu posting, 4 Mar 1997.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















