


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-1-2016
Date: 1-1-2016
Date: 11-1-2016
|
Addition
Addition is one of the first things you learn when beginning math education. In order to add, you must know how to count using traditional counting numbers (1, 2, 3, etc). Once you have a good understanding of counting, you will begin to add numbers together. To start, we’re going to use one digit plus one digit examples, and move on to harder examples.
Adding One Digit Plus One Digit Numbers
Adding one digit to another digit is the first kind of addition problem you’ll learn how to complete. A basic addition problem looks like this:
2 + 1 = _____
In order to complete this problem, you would first count to two, and then count one more (adding it), and get to three. If you were to look at it with pictures instead of numbers, it would look like this:


For beginners, it may be easier to draw dots and then count them all together, like we did for this one. Let’s try this again. Here’s the problem, in numbers and in pictures:

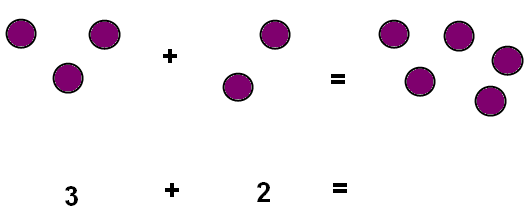
Once you can add simple numbers together, you’ll move on to adding two digit plus one digit numbers. A two digit plus one digit problem would look like this:
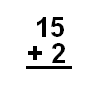
In order to complete this problem, you’re first going to add the ones’ columns together. For this problem, you’d be adding together 5 + 2. You write the answer to this part in the ones’ column under the answer bar. Then, you move on and add the tens’ column together. In this problem, the only number in the tens’ column is 1, so you would bring 1 down and write it in the tens’ column of the answer.
Then, you’re done! Here’s the work for the problem:
Step 1:


Step 2:
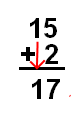

Now, we get our final answer of 17.
Adding Two Digit Plus One Digit Numbers With Carrying
After you add two digit plus one digit numbers for a while, you’ll run into a problem where you have to carry a number. This happens when you get an answer of 10 or more when you add the ones’ column together. For example, if your ones’ column said 9+3, that gives you 12, and you’d need to carry. In order to carry, you need to follow three steps very carefully.
First, after you’ve added and gotten the number, you need to split the number up into two separate digits. You’re not going to write anything yet; you do this step in your head. For example, if you got 12 for your answer to the first part of the problem, you would look at it as 1 and 2 (two separate digits).
Second, you’re going to take the ones’ digit of the number you just split up, and write it in the ones’ column of your answer. (This should seem normal after doing addition without carrying).
Last, here’s the different step: you’re going to take the tens’ digit of the number you just split up, and write it at the top of the tens’ column in your addition problem.
Congrats, you’ve carried! Now let’s see what it looks like in the problem itself:

Now you need to finish the addition problem. All you have left to do is add together the numbers in the tens’ column now. Notice that after you’ve carried, there are now 2 numbers in the tens’ column. In this problem, they are both ones. You would add these two numbers together, and place the answer in the tens’ column of the answer. It would look like this:

Now you have a final answer, 22.
Let’s try this a couple more times to make sure you understand.

Go ahead and try this problem on your own. Remember to split up the answer to the addition of the ones’ column, and put the ones’ digit in the answer while carrying the tens’ digit up to the next column. We’ll show this one more time, but after that we’re not going to write it out.
Adding Two Digit Plus Two Digit Numbers Without Carrying
More advanced addition problems will ask you to add two digit plus two digit numbers. A problem adding together two two-digit numbers looks like this:

This may look a little harder than before, but don’t worry! It’s not too bad. You just have to remember to do it in the right order. First, add together the ones’ column, and write the answer beneath the answer bar, like this:

Then, move over to the tens’ column and write that answer in the tens’ column beneath the answer bar, like this:

The solution would look like this:

Did you get 55? If not, re-add each column to see where your mistake is. Remember to add each column separately in order to get your answer. Your final answer for this problem is 55.
Adding Two Digit Plus Two Digit Numbers With Carrying
Now that you know how to add two digit numbers together, we’re going to practice doing it when you have to carry a number. It works very similarly to the carrying shown previously. Here’s a problem to start with, and we’ll go through each step of solving it.

Start this as you would a normal addition problem, with the ones’ column. Notice when you add the ones’ column together that you get a number higher than ten, which means you have to carry. You’re going to carry the same way as we showed in Adding Two Digit Plus One Digit Numbers With Carrying. Split up the number and write the ones’ digit under the ones’ column beneath the answer bar, and write the tens’ digit above the tens’ column in the addition problem. These steps look like this (the ones’ column is circled in red, and the number in red at the top of the tens’ column is the number that was carried).

Now, you can go ahead and add the tens’ column together. Notice that now there are three numbers in the tens’ column that you must add together, 1 + 3 + 2. Here’s the rest of the solution:

Thus, our final answer is 61.
Let’s try one more example that’s a little bit harder. Here’s the problem:

First, add the ones’ column together. Place the ones’ digit of the answer beneath the answer bar in the ones’ column, and the tens’ digit of the answer above the tens’ column in the division problem.

Now, once again, you have 3 digits in the tens’ column to add together, 1 + 6 + 8. When you add these together, you get 15. Next, you simply write 15 in front of the 6. Now, you have 6 in the ones’ column, 5 in the tens’ column, and 1 in the hundreds’ column. Your solution looks like this (we’ll put the 15 in red so you can see how it lines up):
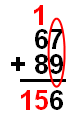
Thus, our final answer is 156.
www.wyzant.com



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|