


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-5-2019
Date: 10-10-2019
Date: 24-6-2019
|
The inverse hyperbolic functions, sometimes also called the area hyperbolic functions (Spanier and Oldham 1987, p. 263) are the multivalued function that are the inverse functions of the hyperbolic functions. They are denoted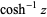 ,
, 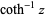 ,
, 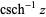 ,
, 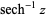 ,
, 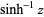 , and
, and 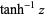 . Variants of these notations beginning with a capital letter are commonly used to denote their principal values (e.g., Harris and Stocker 1998, p. 263).
. Variants of these notations beginning with a capital letter are commonly used to denote their principal values (e.g., Harris and Stocker 1998, p. 263).
These functions are multivalued, and hence require branch cuts in the complex plane. Differing branch cut conventions are possible, but those adopted in this work follow those used by the Wolfram Language, summarized below.
| function name | function | the Wolfram Language | branch cut(s) |
| inverse hyperbolic cosecant | 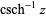 |
ArcCsch[z] | 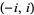 |
| inverse hyperbolic cosine | 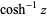 |
ArcCosh[z] | 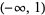 |
| inverse hyperbolic cotangent | 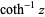 |
ArcCoth[z] | ![[-1,1]](http://mathworld.wolfram.com/images/equations/InverseHyperbolicFunctions/Inline12.gif) |
| inverse hyperbolic secant | 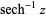 |
ArcSech[z] | ![(-infty,0]](http://mathworld.wolfram.com/images/equations/InverseHyperbolicFunctions/Inline14.gif) and and 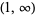 |
| inverse hyperbolic sine | 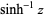 |
ArcSinh[z] | 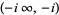 and and 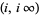 |
| inverse hyperbolic tangent | 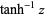 |
ArcTanh[z] | ![(-infty,-1]](http://mathworld.wolfram.com/images/equations/InverseHyperbolicFunctions/Inline20.gif) and and 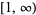 |
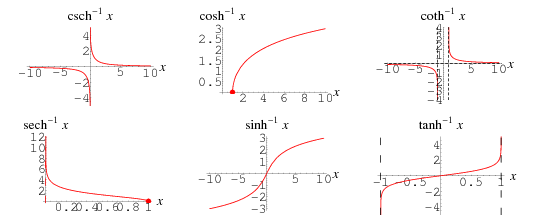
The inverse hyperbolic functions as defined in this work have the following ranges for domains on the real line 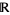 , again following the convention of the Wolfram Language.
, again following the convention of the Wolfram Language.
| function name | function | domain | range |
| inverse hyperbolic cosecant | 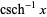 |
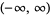 |
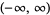 |
| inverse hyperbolic cosine | 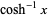 |
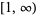 |
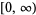 |
| inverse hyperbolic cotangent | 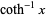 |
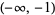 or or 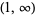 |
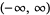 |
| inverse hyperbolic secant | 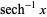 |
![(0,1]](http://mathworld.wolfram.com/images/equations/InverseHyperbolicFunctions/Inline34.gif) |
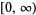 |
| inverse hyperbolic sine | 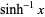 |
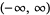 |
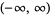 |
| inverse hyperbolic tangent | 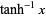 |
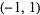 |
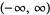 |
They are defined in the complex plane by
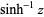 |
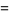 |
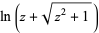 |
(1) |
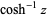 |
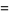 |
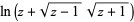 |
(2) |
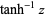 |
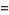 |
![1/2[ln(1+z)-ln(1-z)]](http://mathworld.wolfram.com/images/equations/InverseHyperbolicFunctions/Inline50.gif) |
(3) |
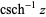 |
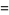 |
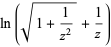 |
(4) |
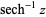 |
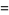 |
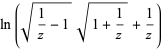 |
(5) |
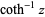 |
 |
![1/2[ln(1+1/z)-ln(1-1/z)].](http://mathworld.wolfram.com/images/equations/InverseHyperbolicFunctions/Inline59.gif) |
(6) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Inverse Hyperbolic Functions." §4.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 86-89, 1972.
Beyer, W. H. "Inverse Hyperbolic Functions." CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 181-186, 1987.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Harris, J. W. and Stocker, H. "Area Hyperbolic Functions." Handbook of Mathematics and Computational Science. New York: Springer-Verlag, pp. 263-273, 1998.
Jeffrey, A. "Inverse Trigonometric and Hyperbolic Functions." §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed.Orlando, FL: Academic Press, pp. 124-128, 2000.
Spanier, J. and Oldham, K. B. "The Inverse Hyperbolic Functions." Ch. 31 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 285-293, 1987.
Trott, M. "Inverse Trigonometric and Hyperbolic Functions." §2.2.5 in The Mathematica GuideBook for Programming. New York: Springer-Verlag, pp. 180-191, 2004. http://www.mathematicaguidebooks.org/.
Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, 1995.



|
|
|
|
دراسة: عدم ترتيب الغرفة قد يدل على مشاكل نفسية
|
|
|
|
|
|
|
علماء: تغير المناخ تسبب في ارتفاع الحرارة خلال موسم الحج
|
|
|
|
|
|
|
جهود مكثفة وطباعة عشرات الآلاف من المنشورات .. استعدادات العتبة العلوية المقدسة لعيد الغدير الأغر
|
|
|