


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-6-2019
Date: 23-7-2019
Date: 30-3-2019
|
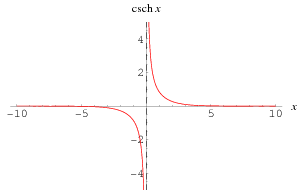

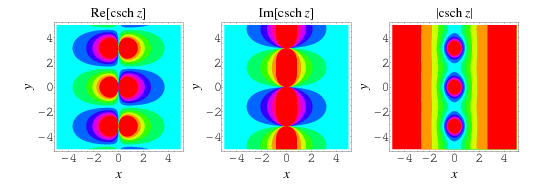
The hyperbolic cosecant is defined as
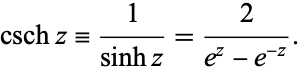 |
(1) |
It is implemented in the Wolfram Language as Csch[z].
It is related to the hyperbolic cotangent though
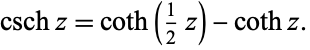 |
(2) |
The derivative is given by
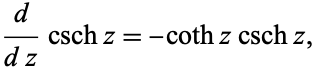 |
(3) |
where 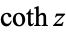 is the hyperbolic cotangent, and the indefinite integral by
is the hyperbolic cotangent, and the indefinite integral by
![intcschzdz=ln[sinh(1/2z)]-ln[cosh(1/2z)]+C,](http://mathworld.wolfram.com/images/equations/HyperbolicCosecant/NumberedEquation4.gif) |
(4) |
where 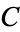 is a constant of integration.
is a constant of integration.
It has Taylor series
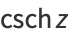 |
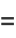 |
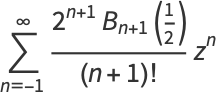 |
(5) |
 |
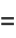 |
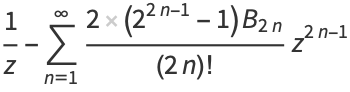 |
(6) |
 |
 |
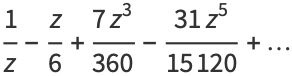 |
(7) |
(OEIS A036280 and A036281), where 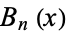 is a Bernoulli polynomial and
is a Bernoulli polynomial and 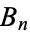 is a Bernoulli number.
is a Bernoulli number.
Sums include
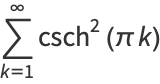 |
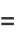 |
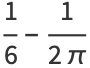 |
(8) |
 |
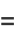 |
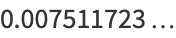 |
(9) |
(OEIS A110191; Berndt 1977).
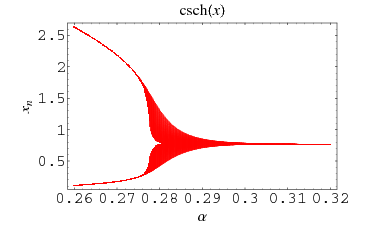
The plot above shows a bifurcation diagram for 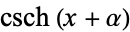 .
.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Hyperbolic Functions." §4.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 83-86, 1972.
Berndt, B. C. "Modular Transformations and Generalizations of Several Formulae of Ramanujan." Rocky Mtn. J. Math. 7, 147-189, 1977.
Jeffrey, A. "Hyperbolic Identities." §2.5 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 117-122, 2000.
Sloane, N. J. A. Sequences A036280, A036281, and A110191 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Hyperbolic Secant 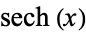 and Cosecant
and Cosecant 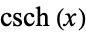 Functions." Ch. 29 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 273-278, 1987.
Functions." Ch. 29 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 273-278, 1987.
Zwillinger, D. (Ed.). "Hyperbolic Functions." §6.7 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 476-481 1995.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|