Lemniscate Function

The lemniscate functions arise in rectifying the arc length of the lemniscate. The lemniscate functions were first studied by Jakob Bernoulli and Giulio Fagnano. A historical account is given by Ayoub (1984), and an extensive discussion by Siegel (1969). The lemniscate functions were the first functions defined by inversion of an integral

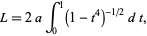(1)

which was first done by Gauss, who noticed that

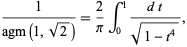(2)

where 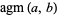 is the arithmetic-geometric mean (Borwein and Bailey 2003, p. 13).

Define the inverse lemniscate functions as

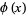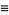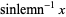			(3)
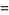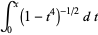			(4)
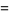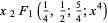			(5)
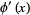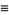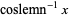			(6)
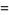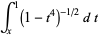			(7)
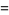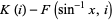			(8)
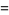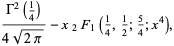			(9)

where 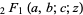 is a hypergeometric function,  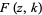is an incomplete elliptic integral of the first kind,  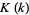is an elliptic integral of the second kind, and

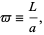(10)

so that

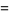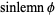			(11)
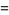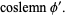			(12)

Now, there is an identity connecting 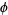 and 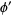 since

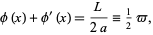(13)

so

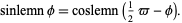(14)

These functions can be written in terms of Jacobi elliptic functions,

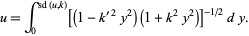(15)

Now, if 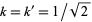, then

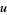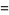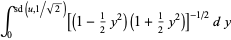			(16)
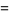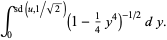			(17)

Let 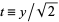 so ,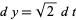

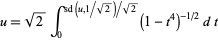(18)

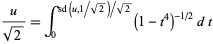(19)

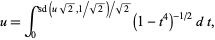(20)

and

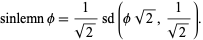(21)

Similarly,

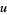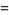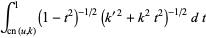			(22)
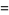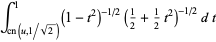			(23)
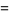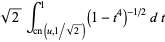			(24)

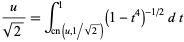(25)

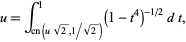(26)

and

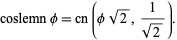(27)

We know

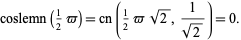(28)

But it is true that

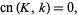(29)

so

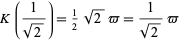(30)

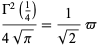(31)

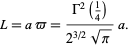(32)

By expanding 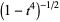 in a binomial series and integrating term by term, the arcsinlemn function can be written

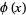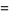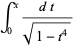			(33)
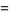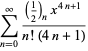			(34)
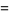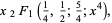			(35)

where 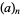 is a Pochhammer symbol (Berndt 1994).

Ramanujan gave the following inversion formula for 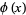. If

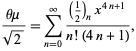(36)

where

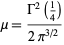(37)

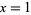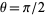is the constant obtained by letting  and , and

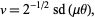(38)

then

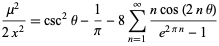(39)

(Berndt 1994).

Ramanujan also showed that if 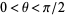, then

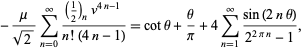(40)

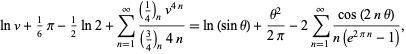(41)

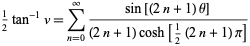(42)

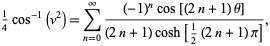(43)

and

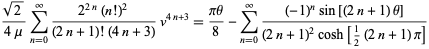(44)

(Berndt 1994).

A generalized version of the lemniscate function can be defined by letting 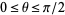 and 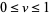. Write

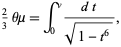(45)

where 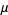 is the constant obtained by setting  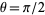and 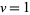. Then

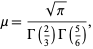(46)

and Ramanujan showed

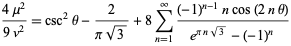(47)

(Berndt 1994).

REFERENCES:

Ayoub, R. "The Lemniscate and Fagnano's Contributions to Elliptic Integrals." Arch. Hist. Exact Sci. 29, 131-149, 1984.

Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 245, and 247-255, 258-260, 1994.

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.

Siegel, C. L. Topics in Complex Function Theory, Vol. 1. New York: Wiley, 1969.