


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-6-2019
Date: 25-8-2018
Date: 6-8-2019
|
There are two types of functions known as Hankel functions. The more common one is a complex function (also called a Bessel function of the third kind, or Weber Function) which is a linear combination of Bessel functions of the first and second kinds.
Another type of Hankel function is defined by the contour integral
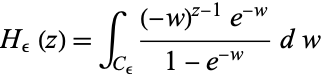 |
for ![I[w]<0](http://mathworld.wolfram.com/images/equations/HankelFunction/Inline1.gif) ,
, 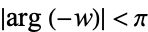 ,
, 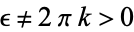 , where
, where 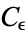 is a Hankel contour. The Riemann zeta function can be expressed in terms of
is a Hankel contour. The Riemann zeta function can be expressed in terms of 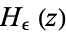 as
as
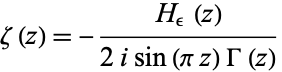 |
for 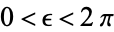 and
and ![R[z]>1](http://mathworld.wolfram.com/images/equations/HankelFunction/Inline7.gif) , where
, where 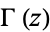 is the gamma function (Krantz 1999, p. 160).
is the gamma function (Krantz 1999, p. 160).
REFERENCES:
Arfken, G. "Hankel Functions." §11.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 604-610, 1985.
Hankel, H. "Die Cylinderfunctionen erster und zweiter Art." Math. Ann. 1, 467-501, 1869.
Hankel, H. "Bestimmte Integrale mit Cylinderfunctionen." Math. Ann. 8, 453-470, 1875.
Krantz, S. G. "The Hankel Contour and Hankel Functions." §13.2.4 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 159, 1999.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 623-624, 1953.A



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|