Fundamental Theorem of Algebra

Every polynomial equation having complex coefficients and degree 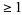 has at least one complex root. This theorem was first proven by Gauss. It is equivalent to the statement that a polynomial  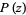of degree  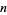has 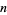 values  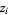(some of them possibly degenerate) for which 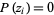. Such values are called polynomial roots. An example of apolynomial with a single root of multiplicity  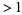is 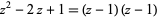, which has  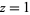as a root of multiplicity 2.

REFERENCES:

Courant, R. and Robbins, H. "The Fundamental Theorem of Algebra." §2.5.4 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 101-103, 1996.

Krantz, S. G. "The Fundamental Theorem of Algebra." §1.1.7 and 3.1.4 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 7 and 32-33, 1999.

Smithies, F. "A Forgotten Paper on the Fundamental Theorem of Algebra." Notes Rec. Roy. Soc. London 54, 333-341, 2000.