


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-11-2018
Date: 27-11-2018
Date: 25-11-2018
|
A hyperfunction, discovered by Mikio Sato in 1958, is defined as a pair of holomorphic functions 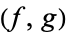 which are separated by a boundary
which are separated by a boundary 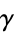 . If
. If 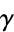 is taken to be a segment on the real-line, then f is defined on the open region
is taken to be a segment on the real-line, then f is defined on the open region 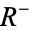 below the boundary and
below the boundary and 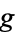 is defined on the open region
is defined on the open region 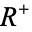 above the boundary. A hyperfunction
above the boundary. A hyperfunction 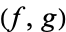 defined on gamma is the "jump" across the boundary from
defined on gamma is the "jump" across the boundary from 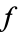 to
to 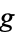 .
.
This 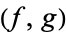 pair forms an equivalence class of pairs of holomorphic functions
pair forms an equivalence class of pairs of holomorphic functions 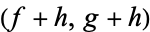 , where
, where 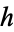 is a holomorphic function defined on the open region
is a holomorphic function defined on the open region 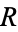 , comprised of both
, comprised of both 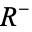 and
and 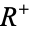 .
.
Hyperfunctions can be shown to satisfy
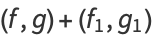 |
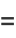 |
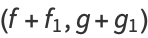 |
(1) |
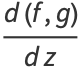 |
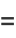 |
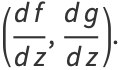 |
(2) |
There is no general product between hyperfunctions, but the product of a hyperfunction by a holomorphic function 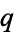 can be expressed as
can be expressed as
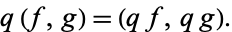 |
(3) |
A standard holomorphic function  can also be defined as a hyperfunction,
can also be defined as a hyperfunction,
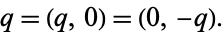 |
(4) |
The Heaviside step function 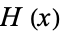 and the delta function
and the delta function 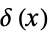 can be defined as the hyperfunctions
can be defined as the hyperfunctions
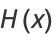 |
 |
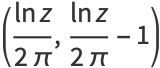 |
(5) |
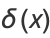 |
 |
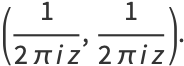 |
(6) |
REFERENCES:
Isao, I. Applied Hyperfunction Theory. Amsterdam, Netherlands: Kluwer, 1992.
Penrose, R. The Road to Reality: A Complete Guide to the Laws of the Universe. New York: Random House, 2006.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|