


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-10-2018
Date: 18-10-2018
Date: 16-12-2018
|
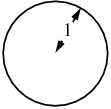
A unit circle is a circle of unit radius, i.e., of radius 1.
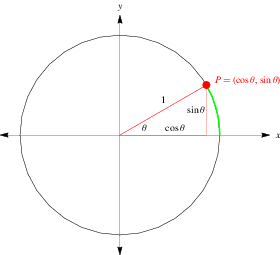
The unit circle plays a significant role in a number of different areas of mathematics. For example, the functions of trigonometry are most simply defined using the unit circle. As shown in the figure above, a point 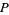 on the terminal side of an angle
on the terminal side of an angle 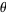 in angle standard position measured along an arc of the unit circle has as its coordinates
in angle standard position measured along an arc of the unit circle has as its coordinates 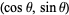 so that
so that 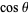 is the horizontal coordinate of
is the horizontal coordinate of 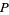 and
and 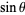 is its vertical component.
is its vertical component.
As a result of this definition, the trigonometric functions are periodic with period 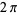 .
.
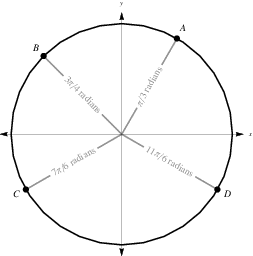
Another immediate result of this definition is the ability to explicitly write the coordinates of a number of points lying on the unit circle with very little computation. In the figure above, for example, points  ,
,  ,
, 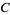 , and
, and 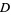 correspond to angles of
correspond to angles of 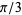 ,
, 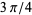 ,
, 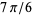 , and
, and 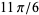 radians, respectively, whereby it follows that
radians, respectively, whereby it follows that 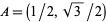 ,
, 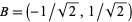 ,
, 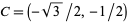 , and
, and 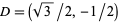 . Similarly, this method can be used to find trigonometric values associated to integer multiples of
. Similarly, this method can be used to find trigonometric values associated to integer multiples of 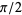 , plus a number of other angles obtained by half-angle, double-angle, and other multiple-angle formulas.
, plus a number of other angles obtained by half-angle, double-angle, and other multiple-angle formulas.
The unit circle can also be considered to be the contour in the complex plane defined by 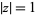 , where
, where 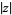 denotes the complex modulus. This role of the unit circle also has a number of significant results, not the least of which occurs in applied complex analysis as the subset of the complex plane where the Z-transform reduces to the discrete Fourier transform.
denotes the complex modulus. This role of the unit circle also has a number of significant results, not the least of which occurs in applied complex analysis as the subset of the complex plane where the Z-transform reduces to the discrete Fourier transform.
From yet another perspective, the unit circle is viewed as the so-called ideal boundary of the two-dimensional hyperbolic plane 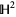 in both the Poincaré hyperbolic disk and Klein-Beltrami models of hyperbolic geometry. In both these models, the hyperbolic plane is viewed as the open unit disk, whereby the unit circle represents the collection of infinite limit points of sequences in
in both the Poincaré hyperbolic disk and Klein-Beltrami models of hyperbolic geometry. In both these models, the hyperbolic plane is viewed as the open unit disk, whereby the unit circle represents the collection of infinite limit points of sequences in 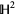 .
.
REFERENCES:
Knopp, K. Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, p. 3, 1996.
Oppenheim, A. V. "The 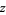 -Transform." 6.003--Signals and Systems. MIT OpenCourseWare, 2011. http://ocw.mit.edu/resources/res-6-007-signals-and-systems-spring-2011/lecture-notes/MITRES_6_007S11_lec23.pdf.
-Transform." 6.003--Signals and Systems. MIT OpenCourseWare, 2011. http://ocw.mit.edu/resources/res-6-007-signals-and-systems-spring-2011/lecture-notes/MITRES_6_007S11_lec23.pdf.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|