


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-11-2018
Date: 25-11-2018
Date: 23-11-2018
|
Let
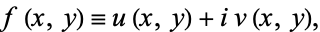 |
(1) |
where
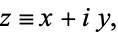 |
(2) |
so
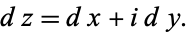 |
(3) |
The total derivative of 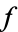 with respect to
with respect to 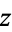 is then
is then
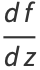 |
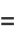 |
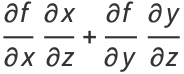 |
(4) |
 |
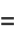 |
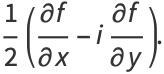 |
(5) |
In terms of 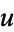 and
and 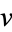 , (5) becomes
, (5) becomes
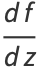 |
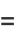 |
![1/2[((partialu)/(partialx)+i(partialv)/(partialx))-i((partialu)/(partialy)+i(partialv)/(partialy))]](http://mathworld.wolfram.com/images/equations/Cauchy-RiemannEquations/Inline13.gif) |
(6) |
 |
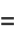 |
![1/2[((partialu)/(partialx)+i(partialv)/(partialx))+(-i(partialu)/(partialy)+(partialv)/(partialy))].](http://mathworld.wolfram.com/images/equations/Cauchy-RiemannEquations/Inline16.gif) |
(7) |
Along the real, or x-axis, 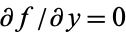 , so
, so
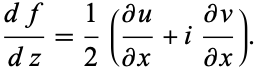 |
(8) |
Along the imaginary, or y-axis, 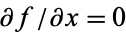 , so
, so
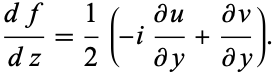 |
(9) |
If 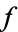 is complex differentiable, then the value of the derivative must be the same for a given
is complex differentiable, then the value of the derivative must be the same for a given 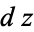 , regardless of its orientation. Therefore, (8) must equal (9), which requires that
, regardless of its orientation. Therefore, (8) must equal (9), which requires that
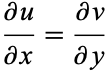 |
(10) |
and
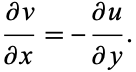 |
(11) |
These are known as the Cauchy-Riemann equations.
They lead to the conditions
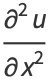 |
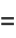 |
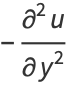 |
(12) |
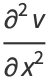 |
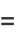 |
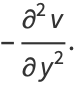 |
(13) |
The Cauchy-Riemann equations may be concisely written as
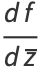 |
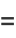 |
![1/2[(partialf)/(partialx)+i(partialf)/(partialy)]](http://mathworld.wolfram.com/images/equations/Cauchy-RiemannEquations/Inline29.gif) |
(14) |
 |
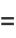 |
![1/2[((partialu)/(partialx)+i(partialv)/(partialx))+i((partialu)/(partialy)+i(partialv)/(partialy))]](http://mathworld.wolfram.com/images/equations/Cauchy-RiemannEquations/Inline32.gif) |
(15) |
 |
 |
![1/2[((partialu)/(partialx)-(partialv)/(partialy))+i((partialu)/(partialy)+(partialv)/(partialx))]](http://mathworld.wolfram.com/images/equations/Cauchy-RiemannEquations/Inline35.gif) |
(16) |
 |
 |
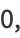 |
(17) |
where 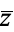 is the complex conjugate.
is the complex conjugate.
If 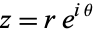 , then the Cauchy-Riemann equations become
, then the Cauchy-Riemann equations become
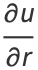 |
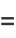 |
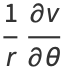 |
(18) |
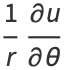 |
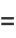 |
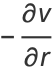 |
(19) |
(Abramowitz and Stegun 1972, p. 17).
If 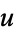 and
and 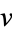 satisfy the Cauchy-Riemann equations, they also satisfy Laplace's equation in two dimensions, since
satisfy the Cauchy-Riemann equations, they also satisfy Laplace's equation in two dimensions, since
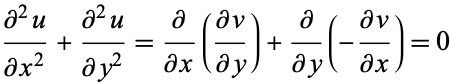 |
(20) |
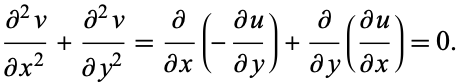 |
(21) |
By picking an arbitrary 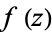 , solutions can be found which automatically satisfy the Cauchy-Riemann equations and Laplace's equation. This fact is used to use conformal mappings to find solutions to physical problems involving scalar potentials such as fluid flow and electrostatics.
, solutions can be found which automatically satisfy the Cauchy-Riemann equations and Laplace's equation. This fact is used to use conformal mappings to find solutions to physical problems involving scalar potentials such as fluid flow and electrostatics.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 17, 1972.
Arfken, G. "Cauchy-Riemann Conditions." §6.2 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 360-365, 1985.
Knopp, K. "The Cauchy-Riemann Differential Equations." §7 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, pp. 28-31, 1996.
Krantz, S. G. "The Cauchy-Riemann Equations." §1.3.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 13, 1999.
Levinson, N. and Redheffer, R. M. Complex Variables. San Francisco, CA: Holden-Day, 1970.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 137, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|