Integration by Parts

Integration by parts is a technique for performing indefinite integration 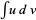 or definite integration  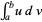by expanding the differential of a product of functions  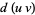and expressing the original integral in terms of a known integral 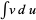. A single integration by parts starts with

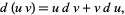(1)

and integrates both sides,

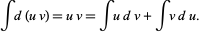(2)

Rearranging gives

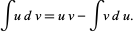(3)

For example, consider the integral 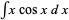 and let

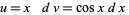	(4)
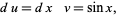	(5)

so integration by parts gives

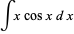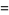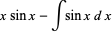			(6)
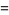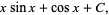			(7)

where 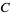 is a constant of integration.

The procedure does not always succeed, since some choices of 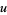 may lead to more complicated integrals than the original. For example, consider again the integral  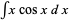and let

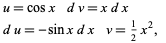(8)

giving

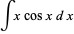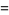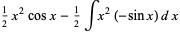			(9)
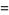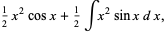			(10)

which is more difficult than the original (Apostol 1967, pp. 218-219).

Integration by parts may also fail because it leads back to the original integral. For example, consider 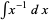 and let

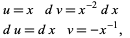(11)

then

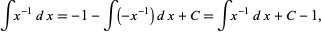(12)

which is same integral as the original (Apostol 1967, p. 219).

The analogous procedure works for definite integration by parts, so

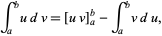(13)

where .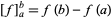

Integration by parts can also be applied 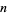 times to :

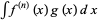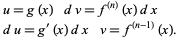(14)

Therefore,

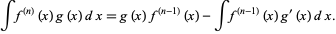(15)

But

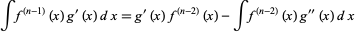(16)

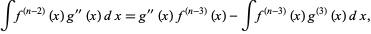(17)

so

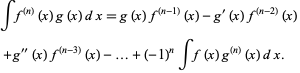(18)

Now consider this in the slightly different form 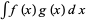. Integrate by parts a first time

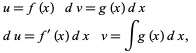(19)

so

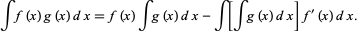(20)

Now integrate by parts a second time,

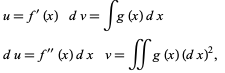(21)

so

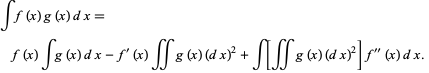(22)

Repeating a third time,

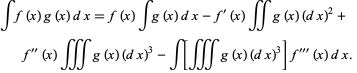(23)

Therefore, after  applications,

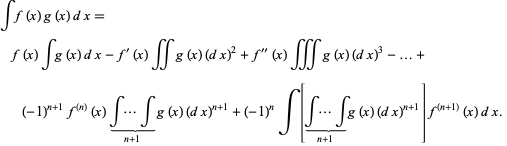(24)

If 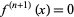 (e.g., for an th degree polynomial), the last term is 0, so the sum terminates after 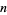 terms and

(25)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.New York: Dover, p. 12, 1972.

Apostol, T. M. "Integration by Parts." §5.9 in Calculus, 2nd ed., Vol. 1: One-Variable Calculus, with an Introduction to Linear Algebra. Waltham, MA: Blaisdell, pp. 217-220, 1967.

Bronshtein, I. N. and Semendyayev, K. A. Handbook of Mathematics, 3rd ed. New York: Springer-Verlag, p. 269, 1997.