


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-9-2018
Date: 22-5-2019
Date: 11-6-2019
|
A volume element is the differential element 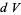 whose volume integral over some range in a given coordinate system gives the volume of a solid,
whose volume integral over some range in a given coordinate system gives the volume of a solid,
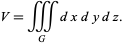 |
(1) |
In 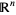 , the volume of the infinitesimal
, the volume of the infinitesimal 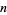 -hypercube bounded by
-hypercube bounded by 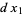 , ...,
, ..., 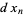 has volume given by the wedge product
has volume given by the wedge product
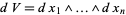 |
(2) |
(Gray 1997).
The use of the antisymmetric wedge product instead of the symmetric product 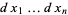 is a technical refinement often omitted in informal usage. Dropping the wedges, the volume element for curvilinear coordinates in
is a technical refinement often omitted in informal usage. Dropping the wedges, the volume element for curvilinear coordinates in 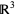 is given by
is given by
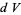 |
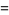 |
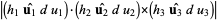 |
(3) |
 |
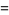 |
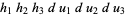 |
(4) |
 |
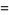 |
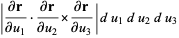 |
(5) |
 |
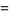 |
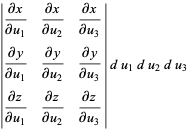 |
(6) |
 |
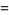 |
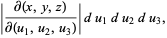 |
(7) |
where the latter is the Jacobian and the 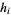 are scale factors.
are scale factors.
REFERENCES:
Gray, A. "Isometries and Conformal Maps of Surfaces." §15.2 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 346-351, 1997.



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
لتعزيز التواصل مع الزائرات الأجنبيات : العتبة العلويّة المقدّسة تُطلق دورة لتعليم اللغة الإنجليزية لخادمات القسم النسويّ
|
|
|