


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-7-2018
Date: 18-7-2018
Date: 23-7-2018
|
A second-order partial differential equation of the form
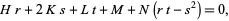 |
(1) |
where 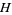 ,
, 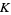 ,
, 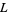 ,
, 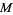 , and
, and 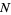 are functions of
are functions of  ,
, 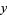 ,
, 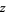 ,
, 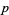 , and
, and 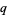 , and
, and 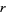 ,
, 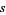 ,
, 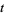 ,
, 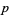 , and
, and 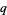 are defined by
are defined by
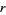 |
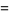 |
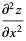 |
(2) |
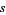 |
 |
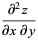 |
(3) |
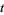 |
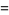 |
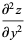 |
(4) |
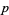 |
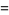 |
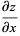 |
(5) |
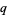 |
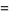 |
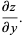 |
(6) |
The solutions are given by a system of differential equations given by Iyanaga and Kawada (1980).
Other equations called the Monge-Ampère equation are
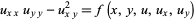 |
(7) |
(Moon and Spencer 1969, p. 171; Zwillinger 1997, p. 134) and
 |
(8) |
(Gilberg and Trudinger 1983, p. 441; Zwillinger 1997, p. 134).
REFERENCES:
Caffarelli, L. A. and Milman, M. Monge Ampère Equation: Applications to Geometry and Optimization.. Providence, RI: Amer. Math. Soc., 1999.
Fairlie, D. B. and Leznov, A. N. "The General Solution of the Complex Monge-Ampère Equation in a Space of Arbitrary Dimension." 16 Sep 1999. http://arxiv.org/abs/solv-int/9909014.
Gilbarg, D. and Trudinger, N. S. Elliptic Partial Differential Equations of Second Order. Berlin: Springer-Verlag, p. 441, 1983.
Iyanaga, S. and Kawada, Y. (Eds.). "Monge-Ampère Equations." §276 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 879-880, 1980.
Moon, P. and Spencer, D. E. Partial Differential Equations. Lexington, MA: Heath, p. 171, 1969.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|