المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Stability Matrix |
 531
 03:03 مساءً
date: 5-7-2018 |
Author : Tabor, M 
Book or Source : "Linear Stability Analysis." §1.4 in Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley 
Page and Part : ...|
Read More
Date: 22-5-2018
1010
Date: 24-5-2018
829
Date: 12-6-2018
988
|
Given a system of two ordinary differential equations
 |
 |
 |
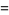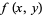(1) |
 |
 |
 |
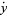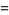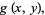(2) |
let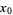 
and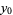 
denote fixed points with 
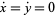, so
 |
 |
 |
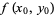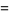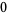(3) |
 |
 |
 |
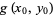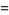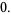(4) |
Then expand about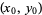 
so
 |
 |
 |
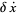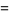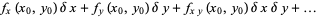(5) |
 |
 |
 |
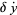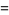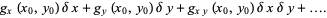(6) |
To first-order, this gives
![d/(dt)[deltax; deltay]=[f_x(x_0,y_0) f_y(x_0,y_0); g_x(x_0,y_0) g_y(x_0,y_0)][deltax; deltay],](http://mathworld.wolfram.com/images/equations/StabilityMatrix/NumberedEquation1.gif) |
(7) |
where the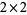 
matrix, or its generalization to higher dimension, is called the stability matrix. Analysis of the eigenvalues (and eigenvectors) of the stability matrix characterizes the type of fixed point.
REFERENCES:
Tabor, M. "Linear Stability Analysis." §1.4 in Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, pp. 20-31, 1989.
|
|
|
|
كيف تساهم الأطعمة فائقة المعالجة في تفاقم مرض يصيب الأمعاء؟
|
|
|
|
|
|
|
مشروع ضخم لإنتاج الهيدروجين الأخضر يواجه تأخيرًا جديدًا
|
|
|
|
|
|
|
المجمع العلمي يختتم دورته القرآنية في فن الصوت والنغم بالطريقة المصرية
|
|
|
