Bessel Differential Equation

The Bessel differential equation is the linear second-order ordinary differential equation given by

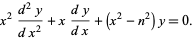(1)

Equivalently, dividing through by ,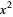

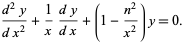(2)

The solutions to this equation define the Bessel functions 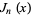 and 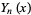. The equation has a regular singularity at 0 and an irregular singularity at .

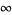A transformed version of the Bessel differential equation given by Bowman (1958) is

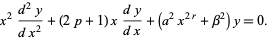(3)

The solution is

(4)

where

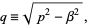(5)

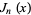 and 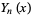 are the Bessel functions of the first and second kinds, an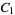d  and 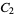 are constants. Another form is given by letting 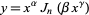, , 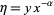and 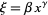 (Bowman 1958, p. 117), then

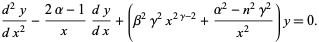(6)

The solution is

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). §9.1.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.

Bowman, F. Introduction to Bessel Functions. New York: Dover, 1958.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 550, 1953.

Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, p. 413, 1995.

Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 121, 1997.