Continuity-nfinite Discontinuity

A real-valued univariate function 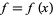 is said to have an infinite discontinuity at a point  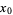in its domain provided that either (or both) of the lower or upper limits of  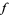fails to exist as  tends to .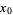

Infinite discontinuities are sometimes referred to as essential discontinuities, phraseology indicative of the fact that such points of discontinuity are considered to be "more severe" than either removable or jump discontinuities.

The figure above shows the piecewise function

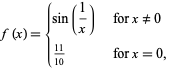(1)

a function for which both 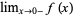 and 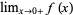 fail to exist. In particular,  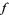has an infinite discontinuity at .

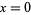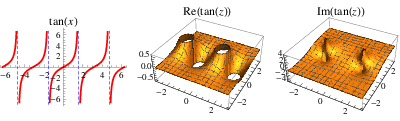
It is not uncommon for authors to say that univariate functions 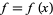 defined on a domain  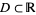and admitting vertical asymptotes of the form  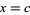have infinite discontinuities there though, strictly speaking, this terminology is incorrect unless such functions are defined piecewise so that 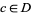. For example, the function  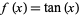has vertical asymptotes at 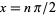, , 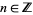though it has no discontinuities of any kind on its domain.

Unsurprisingly, one can extend the above definition to infinite discontinuities of multivariate functions as well

This entry contributed by Christopher Stover .