A matching in a graph is a set of independent edges. That is, it is a set of edges in which no pair shares a vertex. Given a matching M in a graph G, the vertices belonging to the edges of M are said to be saturated by M (or M-saturated). The other vertices are M-unsaturated.

Consider the graph G shown in Figure 1.1. An example of a matching in G is M₁ = {ab, ce, df}. M₂ = {cd, ab} is also a matching, and so is M₃ = {df}.

We can see that a, b, c, d are M₂-saturated and e, f,and g are M₂-unsaturated. The onlyM₁-unsaturated vertex is g.

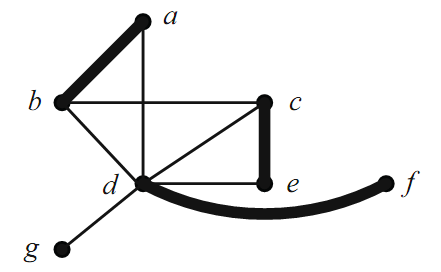
                  FIGURE 1.1. The matching M₁.

If a matching M saturates every vertex of G,then M is said to be a perfect matching. In Figure 1.104, G1 has a perfect matching, namely {ab,ch,de,fg}.

None of G2, G3,and G4 has a perfect matching. Why is this? We will talk more about perfect matchings in Sectionof Perfect Matchings.

A maximum matching in a graph is a matching that has the largest possible cardinality. A maximal matching is a matching that cannot be enlarged by the

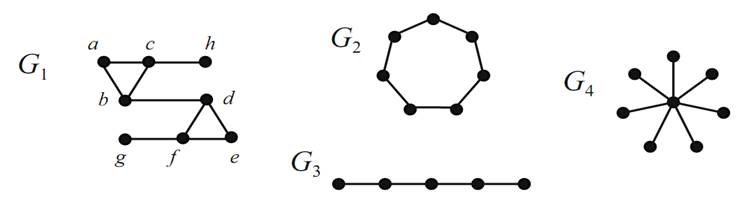
                                     FIGURE 1.2. Only G1 has a perfect matching

addition of any edge. In Figure 1.3, M₁ = {ae,bf,cd,gh} is a maximum matching (since at most one of gh, gi,and gj can be in any matching). The matching  M2 = {dg, af, bc} is maximal, but not maximum.

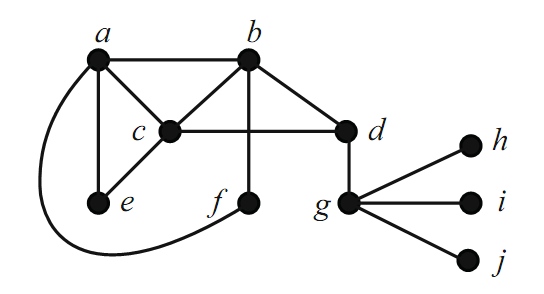
                                 FIGURE 1.3.

Combinatorics and Graph Theory, Second Edition, John M. Harris • Jeffry L. Hirst • Michael J. Mossinghoff,2000,page(101-104)

مواضيع ذات صلة

Minimum Spanning Tree

Maximum Leaf Number

Lobster Graph

Labeled Tree

Internal Path Length

Red-Black Tree

Pseudotree

Pseudoforest

Prüfer Code

Planted Tree

Planted Planar Tree

Graph Strength