الطاقة في مجال مغناطيسي

سنقوم الآن بتعيين الطاقة المختزنة في مجال مغناطيسي ، آخذين في الاعتبار الطاقة المختزنة في ملف محاثة. وسنفترض أن ملف المحاثة هو ملف لولبي طويل. إن المجال المغناطيسي محصورة بالضرورة في قلب الملف اللولبي وله قيمة منتظمة B = μ₀nI.

وقد حسبنا قيمة محاثة ملف لولبي.

L = μ₀n²lA 

حيث l هو طول الملف اللولبي و A مساحة مقطعه المستعرض. ويلاحظ ، مع ذلك أن  lAهو حجم منطقة قلب الملف اللولبي. والطاقة المختزنة داخل الملف اللولبي هي

ومنها نجد أن الطاقة لوحدة الحجوم هي:

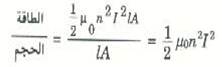
على أن المجال المغناطيسي في الملف اللولبي هو B = μ₀nI ، ومنه ينتج أن I= B/μ₀n وبالتعويض بهذه القيمة في المعادلة السابقة نجد أن

(1)         

وهي تساوي كثافة الطاقة في مجال مغناطيسي شدته B . وعلينا مقارنة هذا المقدار بالمقدار ₀ E²ϵ ½ الذي وجدناه لكثافة الطاقة في مجال كهربائي موجود في الفراغ.

مواضيع ذات صلة

The dipole radiator

Radiation

Electromagnetism

ثنائيات الأشعة السينية آلية عملها

انفجار الأشعة السينية المنبعثة من 1–Sco X

أستاذ المناطيد (مناطيد استكشاف الاشعة السينية)

استعادة التلسكوب الخاص باستكشاف الاشعة السينية من وسط الصحراء: جاك صائد حيوانات الكنغر

التحليق عاليا المناطيد.. وكواشف الأشعة السينية.. وعملية الإطلاق

مطاردة الأشعة السينية بالمناطيد.. البداية

ما هي الأشعة السينية؟

أشعة سينية من الفضاء الخارجي

إنجاز ماكسويل العظيم