
الإنْتروبي Entropy
 المؤلف:
د. نضال الرشيدات
المؤلف:
د. نضال الرشيدات
 المصدر:
دِيناميكا حَراريَّة
المصدر:
دِيناميكا حَراريَّة
 الجزء والصفحة:
ج 5 ص10
الجزء والصفحة:
ج 5 ص10
 17-1-2016
17-1-2016
 1809
1809
الإنْتروبي Entropy
في الفقرة السابقة تعاملنا مع القيم المطلقة للسريان الحراري إلى ومن النظام. إذا كتبنا العلاقة السابقة بأخذ إشارة السريانيْن الحراريَّيْن Q2 > 0 و Q1 < 0 فإنَّه لدورة كارنو:
|
(1-1)
|
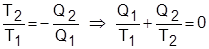
|
لنعتبر عمليَّة دوريَّة منعكسة اعتباطيَّة والمُمثَّلة بالخط المتصل المغلق في الشكل 1. يُمكن تقريب النتائج "الصافية" لهذه العمليَّة المنتهية بعمل عدد كبير جدَّاً من دورات كارنو صغيرة وجميعها في اتجاه واحد (في الشكل اتجاه هذه الدورات هو مع عقارب الساعة- اتجاه الأسهم).
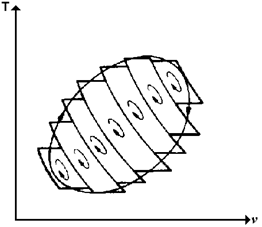
الشكل 1: يُمكن تمثيل أيَّة عمليَّة دوريَّة منعكسة بعدد كبير جدَّاً من دورات كارنو الصغيرة
بالتدقيق في الشكل نجد أنَّ الأجزاء الأدياباتيَّة من الدورات الكارنويَّة تُلغي تأثيرها بعضها الآخر، فالنظام يخضع لعمليَّة أدياباتيَّة في اتجاه ما ثمَّ يمرُّ بنفس العمليَّة في الاتجاه المعاكس، وتكون المُحصِّلة هي الخط المتعرج المتصل في الشكل. كُلَّما كبر عدد الدورات كُلَّما أصبح تأثير إلغاء العمليَّات الأدياباتيَّة أكبر، وتبقى مع ذلك العمليَّات الأيزوحراريَّة التي يحدث خلالها السريان الحراري من وإلى النظام.
إذا نقلتا النظام بيْنَ درجتي الحرارة T2 و T1 وكان السريانان الحراريَّان المرادفان هما ΔQ2 و ΔQ1 فإنَّ:
وعند جمع الحدود المرادف لعدد كبير من الدورات فإنَّ:
حيثُ يدُّل الرمز السفلي r على أنَّ العلاقة السابقة صالحة لدورات منعكسة فقط. وعندما نجعل عدد الدورات كبيراً جدَّاً فإنَّ الخط المتعرج يقترب أكثر فأكثر من الدورة المنعكسة الأصليَّة ويُصبح بالإمكان تحويل الجمع المنفصل (S) في العلاقة السابقة إلى تكامل أي:
|
(1-2)
|

|
مع أنَّ الكميَّة 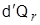 ليست تفاضلاً تامَّاً إلاَّ أنَّ النسبة
ليست تفاضلاً تامَّاً إلاَّ أنَّ النسبة 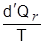 تفاضلٌ تامٌّ، تماماً مثلها مثل dU و dV لأنَّ تكاملها عبر مسار مغلق يُساوي صفراً. يُمكن إذاً أنَّ نُعرِّف خاصيَّة S للنظام تعتمد قيمتها على حالة النظام وتفاضلها هو:
تفاضلٌ تامٌّ، تماماً مثلها مثل dU و dV لأنَّ تكاملها عبر مسار مغلق يُساوي صفراً. يُمكن إذاً أنَّ نُعرِّف خاصيَّة S للنظام تعتمد قيمتها على حالة النظام وتفاضلها هو:
|
(1-3)
|
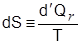
|
وبالتالي في عمليَّة دورية:
|
(1-4)
|

|
لا يعتمد تكامل التفاضل التام على المسار المتبع وبالتالي فإنَّ تكامل التفاضل dS بيْنَ حالتي اتزان للنظام يعتمد فقط على نقطتي البداية والنهاية، أو:
|
(1-5)
|
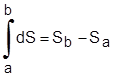
|
تُسمَّى الخاصيَّة S إنْتروبي النظام ووحدتها في نظام MKS هي J K-1. الإنْتروبي مثل الحجم خاصيَّة ممتدَّة، أي تعتمد على الكتلة ونُعرِّف الإنْتروبي النوعيَّة 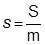 ووحدتها J K-1 kg-1 و الإنْتروبي النوعيَّة الموليَّة
ووحدتها J K-1 kg-1 و الإنْتروبي النوعيَّة الموليَّة  ووحدتها J K-1 kilomole-1.
ووحدتها J K-1 kilomole-1.
تُعرِّف العلاقتان 1-3 و 1-5 الفرق في الإنْتروبي بيْنَ حالتيْن وليس الإنْتروبي في نقطة والتي نحتاج لتعريفها إلى نقطة مرجع حسب هاتيْن العلاقتيْن أي أنَّه يُمكن تعريف الإنْتروبي في نقطة إلاَّ إلى ثابت ما. سوف نرى أنَّه بالإمكان تعريف قيمة مطلقة لإنْتروبي بعض الأنظمة.
 الاكثر قراءة في الكيمياء الحرارية
الاكثر قراءة في الكيمياء الحرارية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


