Character tables

Key point: The systematic analysis of the symmetry properties of molecules is carried out using character tables. We have seen how the symmetry properties of a molecule define its point group and how that point group is labelled by its Schoen flies symbol. Associated with each point group is

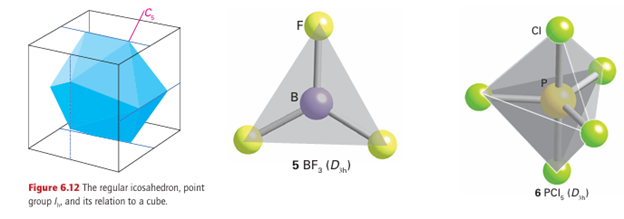
a character table. A character table displays all the symmetry elements of the point group together with a description, as we explain below, of how various objects or mathematical functions transform under the corresponding symmetry operations. A character table is complete: every possible object or mathematical function relating to the molecule belong ing to a particular point group must transform like one of the rows in the character table of that point group.

The structure of a typical character table is shown in Table 6.3. The entries in the main part of the table are called characters,x (chi). Each character shows how an object or mathematical function, such as an atomic orbital, is affected by the corresponding symmetry operation of the group. Thus:

For instance, the rotation of a pz orbital about the z axis leaves it apparently unchanged (hence its character is 1); a reflection of a pz orbital in the xy plane changes its sign (char acter –1). In some character tables, numbers such as 2 and 3 appear as characters: this feature is explained later. The class of an operation is a specific grouping of symmetry operations of the same geometrical type: the two (clockwise and anticlockwise) threefold rotations about an axis form one class, reflections in a mirror plane form another, and so on. The number of members of each class is shown in the heading of each column of the table, as in 2C₃, denoting that there are two members of the class of threefold rotations. All operations of the same class have the same character. Each row of characters corresponds to a particular irreducible representation of the group. An irreducible representation has a technical meaning in group theory but, broadly speaking, it is a fundamental type of symmetry in the group (like the symmetries represented

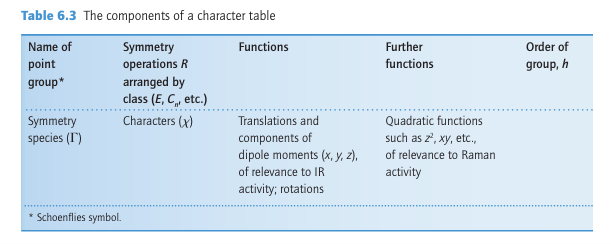
By Ϭ and π orbitals for linear molecules). The label in the first column is the symmetry species (essentially, a label, like and π) of that irreducible representation. The two columns on the right contain examples of functions that exhibit the characteristics of each symmetry species. One column contains functions defined by a single axis, such as translations or p orbitals (x, y, z) or rotations (Rx, Ry, Rz), and the other column contains quadratic functions such as d orbitals (xy, etc). Character tables for a selection of common point groups are given in Resource section 4.

The letter A used to label a symmetry species in the group C_2v means that the function to which it refers is symmetric with respect to rotation about the twofold axis (that is, its character is 1). The label B indicates that the function changes sign under that rotation (the character is –1). The subscript 1 on A1 means that the function to which it refers is also symmetric with respect to reflection in the principal vertical plane (for H2 O this is the plane that contains all three atoms). A subscript 2 is used to denote that the function changes sign under this reflection. Now consider the slightly more complex example of NH₃, which belongs to the point group C_3v (Table 6.5). An NH3 molecule has higher symmetry than H₂O. This higher symmetry is apparent by noting the order, h, of the group, the total number of symmetry operations that can be carried out. For H₂O, h = 4 and for NH₃, h= 6. For highly symmetric molecules, h is large; for example h = 48 for the point group Oh.

 Inspection of the NH3 molecule (Fig. 6.13) shows that whereas the N2pz orbital is unique (it has A1 symmetry), the N2p_x and N2p_y orbitals both belong to the symmetry representation E. In other words, the N2p_x and N2p_y orbitals have the same symmetry characteristics, are degenerate, and must be treated together. The characters in the column headed by the identity operation E give the degeneracy of the orbitals:

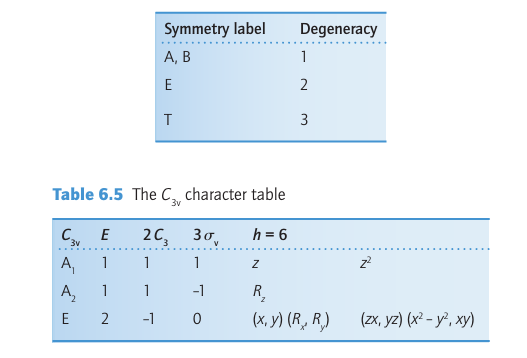
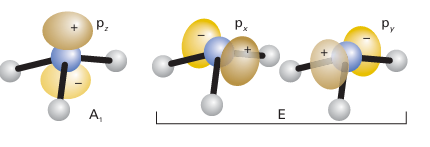
Figure 6.13 The nitrogen 2pz orbital in ammonia is symmetric under all operations of the C_3v point group and therefore has A1 symmetry. The 2p_x and 2p_y orbitals behave identically under all operations (they cannot be distinguished) and are given the symmetry label E.

Be careful to distinguish the italic E for the operation and the roman E for the label: all operations are italic and all labels are roman. Degenerate irreducible representations also contain zero values for some operations because the character is the sum of the characters for the two or more orbitals of the set, and if one orbital changes sign but the other does not, then the total character is 0. For ex ample, the reflection through the vertical mirror plane containing the y-axis in NH₃ results in no change of the py orbital, but an inversion of the p_x orbital.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الخدمية يجري أعمال صيانة دورية لعربات ذوي الاحتياجات الخاصة

جمعية العميد تشارك في اجتماع المجلس الأعلى للجمعيات العلمية العراقية لعام 2025

الهيأة العليا لإحياء التراث تنظم دورة تدريبية عن عرافة الحفل

قسم الصناعات والحرف الفنية يباشر بإنشاء موقع أكاديمية الإعداد البدني

المزيد

الآخبار الصحية

لا تبحث عن الدواء.. هذه الأطعمة كفيلة بإيقاف ألم الرأس

لا تترك زجاجة الماء في السيارة.. احذر شربها

عادة يومية.. كيف يؤثر تصفيف الشعر على جهازك التنفسي؟

احذر هذه الأطعمة.. تسرع الشيخوخة وتفقد بشرتك شبابها

المزيد

الآخبار التكنلوجية

الأوكتان وتأثيره: نصائح لحماية محرك سيارتك بكفاءة وأمان

حرب شهر سبتمبر تشتعل.. ماذا في جعبة أبل وسامسونغ؟

واتساب يطلق ميزة لتعديل الرسائل بالذكاء الاصطناعي

على الكوكب الأحمر.. ناسا تعثر على "قبعة الساحرة"

المزيد

مواضيع ذات صلة

The assignment of molecular symmetry from vibrational spectra

Information from the symmetries of normal modes

The exclusion rule

Molecular vibrations

Chiral molecules

Polar molecules

Symmetry operations, elements and point groups

The stability field of water

Standard potentials and spontaneity

Heterogeneous acid–base reactions

Superacids and superbases

Acidic and neutral solvents