Isaac Newton

Continual Thought
In his later years, Isaac Newton was asked how he had arrived at his theory of universal gravitation. “By thinking on it continually,” was his matter-of-fact response. “Continual thinking” for Newton was almost beyond mortal capacity. He could abandon himself to his studies with a passion and ecstasy that others experience in love affairs. The object of his study could become an obsession, possessing him nonstop, and leaving him without food or sleep, beyond fatigue, and on the edge of breakdown.
The world Newton inhabited in his ecstasy was vast. Richard Westfall, Newton's principal biographer in this century, describes this “world of thought”: “Seen from afar, Newton's intellectual life appears unimaginably rich. He embraced nothing less than the whole of natural philosophy [science], which he explored from several vantage points, ranging all the way from mathematical physics to alchemy. Within natural philosophy, he gave new direction to optics, mechanics, and celestial dynamics, and he invented the mathematical tool [calculus] that has enabled modern science further to explore the paths he first blazed. He sought as well to plumb the mind of God and His eternal plan for the world and humankind as it was presented in the biblical prophecies.”
But, after all, Newton was human. His passion for an investigation would fade, and without synthesizing and publishing the work, he would move on to another grand theme. “What he thought on, he thought on continually, which is to say exclusively, or nearly exclusively,” Westfall continues, but “[his] career was episodic.” To build a coherent whole, Newton sometimes revisited a topic several times over a period of decades.
Woolsthorpe
Newton was born on Christmas Day, 1642, at Woolsthorpe Manor, near the Lincolnshire village of Colsterworth, sixty miles northwest of Cambridge and one hundred miles from London. Newton's father, also named Isaac, died three months before his son's birth. The fatherless boy lived with his mother, Hannah, for three years. In 1646, Hannah married Barnabas Smith, the elderly rector of North Witham, and moved to the nearby rectory, leaving young Isaac behind at Woolsthorpe to live with his maternal grandparents, James and Mary Ayscough. Smith was prosperous by seventeenth-century standards, and he compensated the Ayscoughs by paying for extensive repairs at Woolsthorpe.
Newton appears to have had little affection for his stepfather, his grandparents, his half-sisters and half-brother, or even his mother. In a self-imposed confession of sins, made after he left Woolsthorpe for Cambridge, he mentions “Peevishness with my mother,” “with my sister,” “Punching my sister,” “Striking many,” “Threatning my father and mother Smith to burne them and the house over them,” “wishing death and hoping it to some.”
In 1653, Barnabas Smith died, Hannah returned to Woolsthorpe with the three Smith children, and two years later Isaac entered grammar school in Grantham, about seven miles from Woolsthorpe. In Grantham, Newton's genius began to emerge, but not at first in the classroom. In modern schools, scientific talent is often first glimpsed as an outstanding aptitude in mathematics. Newton did not have that opportunity; the standard English grammar school curriculum of the time offered practically no mathematics. Instead, he displayed astonishing mechanical ingenuity. William Stukely, Newton's first biographer, tells us that he quickly grasped the construction of a windmill and built a working model, equipped with an alternate power source, a mouse on a treadmill. He constructed a cart that he could drive by turning a crank. He made lanterns from “crimpled paper” and attached them to the tails of kites. According to Stukely, this stunt “Wonderfully affrighted all the neighboring inhabitants for some time, and caus'd not a little discourse on market days, among the country people, when over their mugs of ale.”
Another important extracurricular interest was the shop of the local apothecary, remembered only as “Mr. Clark.” Newton boarded with the Clark family, and the shop became familiar territory. The wonder of the bottles of chemicals on the shelves and the accompanying medicinal formulations would help direct him to later interests in chemistry, and beyond that to alchemy.
With the completion of the ordinary grammar school course of studies, Newton reached a crossroads. Hannah felt that he should follow in his father's footsteps and manage the Woolsthorpe estate. For that he needed no further education, she insisted, and called him home. Newton's intellectual promise had been noticed, however. Hannah's brother, William Ayscough, who had attended Cambridge, and the Grantham schoolmaster, John Stokes, both spoke persuasively on Newton's behalf, and Hannah relented. After nine months at home with her restless son, Hannah no doubt recognized his ineptitude for farm management. It probably helped also that Stokes was willing to waive further payment of the forty-shilling fee usually charged for nonresidents of Grantham. Having passed this crisis, Newton returned in 1660 to Grantham and prepared for Cambridge.
Cambridge
Newton entered Trinity College, Cambridge, in June 1661, as a “subsizar,” meaning that he received free board and tuition in exchange for menial service. In the Cambridge social hierarchy, sizars and subsizars were on the lowest level. Evi dently Hannah Smith could have afforded better for her son, but for some reason (possibly parsimony) chose not to make the expenditure.
With his lowly status as a subsizar, and an already well developed tendency to introversion, Newton avoided his fellow students, his tutor, and most of the Cambridge curriculum (centered largely on Aristotle). Probably with few regrets, he went his own way. He began to chart his intellectual course in a “Philosophical Notebook,” which contained a section with the Latin title Quaestiones quaedam philosophicam (Certain Philosophical Questions) in which he listed and discussed the many topics that appealed to his unbounded curiosity. Some of the entries were trivial, but others, notably those under the headings “Motion” and “Colors,” were lengthy and the genesis of later major studies.
After about a year at Cambridge, Newton entered, almost for the first time, the field of mathematics, as usual following his own course of study. He soon traveled far enough into the world of seventeenth-century mathematical analysis to initiate his own explorations. These early studies would soon lead him to a geometrical demonstration of the fundamental theorem of calculus.
Beginning in the summer of 1665, life in Cambridge and in many other parts of England was shattered by the arrival of a ghastly visitor, the bubonic plague. For about two years the colleges were closed. Newton returned to Woolsthorpe, and took with him the many insights in mathematics and natural philosophy that had been rapidly unfolding in his mind.
Newton must have been the only person in England to recall the plague years 1665–66 with any degree of fondness. About fifty years later he wrote that “in those days I was in the prime of my age for invention & minded Mathematicks & Philosophy more then than at any time since.” During these “miracle years,” as they were later called, he began to think about the method of fluxions (his version of calculus), the theory of colors, and gravitation. Several times in his later years Newton told visitors that the idea of universal gravitation came to him when he saw an apple fall in the garden at Woolsthorpe; if gravity brought th apple down, he thought, why couldn’t it reach higher, as high as the Moon?
These ideas were still fragmentary, but profound nevertheless. Later they would be built into the foundations of Newton's most important work. “The miracle,” says Westfall, “lay in the incredible program of study undertaken in private and prosecuted alone by a young man who thereby assimilated the achievement of a century and placed himself at the forefront of European mathematics and science.”
Genius of this magnitude demands, but does not always receive, recognition. Newton was providentially lucky. After graduation with a bachelor's degree, the only way he could remain at Cambridge and continue his studies was to be elected a fellow of Trinity College. Prospects were dim. Trinity had not elected fellows for three years, only nine places were to be filled, and there were many candidates. Newton was not helped by his previous subsizar status and unorthodox program of studies. But against all odds, he was included among the elected. Evidently he had a patron, probably Humphrey Babington, who was related to Clark, the apothecary in Grantham, and a senior fellow of Trinity.
The next year after election as a “minor” fellow, Newton was awarded the Master of Arts degree and elected a “major” fellow. Then in 1668, at age twenty seven and still insignificant in the college, university, and scientific hierarchy, he was appointed Lucasian Professor of Mathematics. His patron for this surprising promotion was Isaac Barrow, who was retiring from the Lucasian chair and expecting a more influential appointment outside the university. Barrow had seen enough of Newton's work to recognize his brilliance.
Newton's Trinity fellowship had a requirement that brought him to another serious crisis. To keep his fellowship he regularly had to affirm his belief in the articles of the Anglican Church, and ultimately be ordained a clergyman. Newton met the requirement several times, but by 1675, when he could no longer escape the ordination rule, his theological views had taken a turn toward heterodoxy, even heresy. In the 1670s Newton immersed himself in theological studies that eventually led him to reject the doctrine of the Trinity. This was heresy, and if admitted, meant the ruination of his career. Although Newton kept his heretical views secret, ordination was no longer a possibility, and for a time, his Trinity fellowship and future at Cambridge appeared doomed.
But providence intervened, once again in the form of Isaac Barrow. Since leaving Cambridge, Barrow had served as royal chaplain. He had the connections at Court to arrange a royal dispensation exempting the Lucasian Professor from the ordination requirement, and another chapter in Newton's life had a happy ending.
Critics
Newton could not stand criticism, and he had many critics. The most prominent and influential of these were Robert Hooke in England, and Christiaan Huygens and Gottfried Leibniz on the Continent.
Hooke has never been popular with Newton partisans. One of his contemporaries described him as “the most ill-natured, conceited man in the world, hated and despised by most of the Royal Society, pretending to have all other inventions when once discovered by their authors.” There is a grain of truth in this concerning Hooke's character, but he deserves better. In science he made contributions to optics, mechanics, and even geology. His skill as an inventor was renowned, and he was a surveyor and an architect. In personality, Hooke and Newton were polar opposites. Hooke was a gregarious extrovert, while Newton, at least during his most creative years, was a secretive introvert. Hooke did not hesitate to rush into print any ideas that seemed plausible. Newton shaped his concepts by thinking about them for years, or even decades. Neither man could bear to acknowledge any influence from the other. When their interests overlapped, bitter confrontations were inevitable.
Among seventeenth-century physicists, Huygens was most nearly Newton's equal. He made important contributions in mathematics. He invented the pendulum clock and developed the use of springs as clock regulators. He studied telescopes and microscopes and introduced improvements in their design. His studies in mechanics touched on statics, hydrostatics, elastic collisions, projectile motion, pendulum theory, gravity theory, and an implicit force concept, including the concept of centrifugal force. He pictured light as a train of wave fronts transmitted through a medium consisting of elastic particles. In matters relating to physics, this intellectual menu is strikingly similar to that of Newton. Yet Huygens's influence beyond his own century was slight, while Newton's was enormous. One of Huygens's limitations was that he worked alone and had few disciples. Also, like Newton, he often hesitated to publish, and when the work finally saw print others had covered the same ground. Most important, however, was his philosophical bias. He followed Rene Descartes in the belief that natural phenomena must have mechanistic explanations. He rejected Newton’s theory of universal gravitation, calling it “absurd,” because it was no more than mathematics and proposed no mechanisms.
Leibniz, the second of Newton's principal critics on the Continent, is remembered more as a mathematician than as a physicist. Like that of Huygens, his physics was limited by a mechanistic philosophy. In mathematics he made two major contributions, an independent (after Newton's) invention of calculus, and an early development of the principles of symbolic logic. One manifestation of Leibniz's calculus can be seen today in countless mathematics and physics textbooks: his notation. The basic operations of calculus are differentiation and integration, accomplished with derivatives and integrals. The Leibniz symbols for derivatives (e.g. dy/dx) and integrals (e.g., ∫ y dx) have been in constant use for more than three hundred years. Unlike many of his scientific colleagues, Leibniz never held an academic post. He was everything but an academic, a lawyer, statesman, diplomat, and professional genealogist, with assignments such as arranging peace negotiations, tracing royal pedigrees, and mapping legal reforms. Leibniz and Newton later engaged in a sordid clash over who invented calculus first.
Calculus Lessons
The natural world is in continuous, never-ending flux. The aim of calculus is to describe this continuous change mathematically. As modern physicists see it, the methods of calculus solve two related problems. Given an equation that expresses a continuous change, what is the equation for the rate of the change? And, conversely, given the equation for the rate of change, what is the equation for the change? Newton approached calculus this way, but often with geometrical arguments that are frustratingly difficult for those with little geometry. I will avoid Newton's complicated constructions and present here for future reference a few rudimentary calculus lessons more in the modern style.
Suppose you want to describe the motion of a ball falling freely from the Tower in Pisa. Here the continuous change of interest is the trajectory of the ball, expressed in the equation
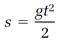 (1)
(1)
in which t represents time, s the ball's distance from the top of the tower, and g a constant we will interpret later as the gravitational acceleration. One of the problems of calculus is to begin with equation (1) and calculate the ball’s rate of fall at every instant.
This calculation is easily expressed in Leibniz symbols. Imagine that the ball is located a distance s from the top of the tower at time t, and that an instant later, at time t + dt, it is located at s + ds; the two intervals dt and ds, called “differentials” in the terminology of calculus, are comparatively very small. We have equation (1) for time t at the beginning of the instant. Now write the equation for time t + dt at the end of the instant, with the ball at s + ds,
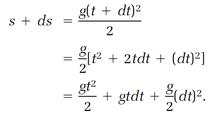 (2)
(2)
Notice the term s on the left side of the last equation and the term gt2/2 the right. According to equation (1), these terms are equal, so they can be canceled from the last equation, leaving
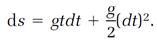 (3)
(3)
In the realm where calculus operates, the time interval dt is very small, and (dt)2 is much smaller than that. (Squares of small numbers are much smaller numbers; for example, compare 0.001 with (0.001)2 = 0.000001.) Thus the term containing (dt)2 in equation (3) is much smaller than the term containing dt, in fact, so small it can be neglected, and equation (3) finally reduces to
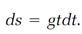 (4)
(4)
Dividing by the dt factor on both sides of this equation, we have finally
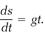 (5)
(5)
(As any mathematician will volunteer, this is far from a rigorous account of the workings of calculus.)
This result has a simple physical meaning. It calculates the instantaneous speed of the ball at time t. Recall that speed is always calculated by dividing a distance interval by a time interval. (If, for example, the ball falls 10 meters at constant speed for 2 seconds, its speed is 10/2= 5 meters per second.) In equation
(5), the instantaneous distance and time intervals ds and dt are divided to calculate the instantaneous speed ds/dt.
The ratio ds/dt in equation (5) is called a “derivative,” and the equation, like any other containing a derivative, is called a “differential equation.” In mathematical physics, differential equations are ubiquitous. Most of the theories mentioned in this book rely on fundamental differential equations. One of the rules of theoretical physics is that (with a few exceptions) its laws are most concisely stated in the common language of differential equations.
The example has taken us from equation (1) for a continuous change to equation (5) for the rate of the change at any instant. Calculus also supplies the means to reverse this argument and derive equation (1) from equation (5). The first step is to return to equation (4) and note that the equation calculates only one differential step, ds, in the trajectory of the ball. To derive equation (1) we must add all of these steps to obtain the full trajectory. This summation is an “integration” operation and in the Leibniz notation it is represented by the elongated-S symbol ʃ. For integration of equation (4) we write
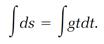 (6)
(6)
We know that this must be equivalent to equation (1), so we infer that the rules for evaluating the two “integrals” in equation (6) are
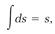 (7)
(7)
and
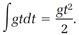 (8)
(8)
Integrals and integration are just as fundamental in theoretical physics as differential equations. Theoreticians usually compose their theories by first writing differential equations, but those equations are likely to be inadequate for the essential further task of comparing the predictions of the theory with experimental and other observations. For that, integrated equations are often a necessity. The great misfortune is that some otherwise innocent-looking differential equations are extremely difficult to integrate. In some important cases (including one Newton struggled with for many years, the integration of the equations of motion for the combined system comprising Earth, the Moon, and the Sun), the equations cannot be handled at all without approximations.
A glance at a calculus textbook will reveal the differentiation rule used to arrive at equation (5), the integration rules (7) and (8), and dozens of others. As its name implies, calculus is a scheme for calculating, in particular for calculations involving derivatives and differential equations. The scheme is organized around the differentiation and integration rules.
Calculus provides a perfect mathematical context for the concepts of mechanics. In the example, the derivative ds/dt calculates a speed. Any speed v is calculated the same way,
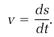 (9)
(9)
If the speed changes with time if there is an acceleration that can be expressed as the rate of change in v, as the derivative dv/dt. So the acceleration differential equation is
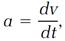 (10)
(10)
in which a represents acceleration. The freely falling ball accelerates, that is, its speed increases with time, as equation (5) combined with equation (9), which is written
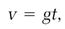 (11)
(11)
shows. The constant factor g is the acceleration of free fall, that is, the gravitational acceleration.
This discussion has used the Leibniz notation throughout. Newton's calculus notation was similar but less convenient. He emphasized rates of change with time, called them “fluxions,” and represented them with an overhead dot notation. For example, in Newton's notation, equation (5) becomes
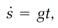
in which s, Newton's symbol for ds/dt , is the distance fluxion, and equation (10) is
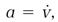
With ύ representing dv/dt, the speed fluxion.
Optics
The work that first brought Newton to the attention of the scientific community was not a theoretical or even a mathematical effort; it was a prodigious technical achievement. In 1668, shortly before his appointment as Lucasian Professor, Newton designed and constructed a “reflecting” telescope. In previous telescopes, beginning with the Dutch invention and Galileo's improvement, light was refracted and focused by lenses. Newton's telescope reflected and focused light with a concave mirror. Refracting telescopes had limited resolution and to achieve high magnification had to be inconveniently long. (Some refracting telescopes at the time were a hundred feet long, and a thousand-footer was planned.) Newton's design was a considerable improvement on both counts.
Newton's telescope project was even more impressive than that of Galileo. With no assistance (Galileo employed a talented instrument maker), Newton cast and ground the mirror, using a copper alloy he had prepared, polished the mirror, and built the tube, the mount, and the fittings. The finished product was just six inches in length and had a magnification of forty, equivalent to a refracting telescope six feet long.
Newton was not the first to describe a reflecting telescope. James Gregory, professor of mathematics at St. Andrews University in Scotland, had earlier published a design similar to Newton's, but could not find craftsmen skilled enough to construct it.
No less than Galileo's, Newton's telescope was vastly admired. In 1671, Barrow demonstrated it to the London gathering of prominent natural philosophers known as the Royal Society. The secretary of the society, Henry Oldenburg, wrote to Newton that his telescope had been “examined here by some of the most eminent in optical science and practice, and applauded by them.” Newton was promptly elected a fellow of the Royal Society.
Before the reflecting telescope, Newton had made other major contributions in the field of optics. In the mid-1660s he had conceived a theory that held that ordinary white light was a mixture of pure colors ranging from red, through orange, yellow, green, and blue, to violet, the rainbow of colors displayed by a prism when it receives a beam of white light. In Newton's view, the prism separated the pure components by refracting each to a different extent. This was a contradiction of the prevailing theory, advocated by Hooke, among others, that light in the purest form is white, and colors are modifications of the pristine white light.
Newton demonstrated the premises of his theory in an experiment employing two prisms. The first prism separated sunlight into the usual red-through-violet components, and all of these colors but one were blocked in the beam received by the second prism. The crucial observation was that the second prism caused no further modification of the light. “The purely red rays refracted by the second prism made no other colours but red,” Newton observed in 1666, “& the purely blue no other colours but blue ones.” Red and blue, and other colors produced by the prism, were the pure colors, not the white.
Soon after his sensational success with the reflecting telescope in 1671, Newton sent a paper to Oldenburg expounding this theory. The paper was read at a meeting of the Royal Society, to an enthusiastically favorable response. Newton was then still unknown as a scientist, so Oldenburg innocently took the additional step of asking Robert Hooke, whose manifold interests included optics, to comment on Newton's theory. Hooke gave the innovative and complicated paper about three hours of his time, and told Oldenburg that Newton's arguments were not convincing.
This response touched off the first of Newton's polemical battles with his critics. His first reply was restrained; it prompted Hooke to give the paper in question more scrutiny, and to focus on Newton's hypothesis that light is particle-like. (Hooke had found an inconsistency here; Newton claimed that he did not rely on hypotheses.) Newton was silent for a while, and Hooke, never silent, claimed that he had built a reflecting telescope before Newton. Next, Huygens and a Jesuit priest, Gaston Pardies, entered the controversy. Apparently in support of Newton, Huygens wrote, “The theory of Mr. Newton concerning light and colors appears highly ingenious to me.” In a communication to the Philosophical Transactions of the Royal Society, Pardies questioned Newton's prism experiment, and Newton’s reply, which also appeared in the Transactions, was condescending. Hooke complained to Oldenburg that Newton was demeaning the debate, and Oldenburg wrote a cautionary letter to Newton. By this time, Newton was aroused enough to refute all of Hooke's objections in a lengthy letter to the Royal Society, later published in the Transactions. This did not quite close the dispute; in a final episode, Huygens reentered the debate with criticisms similar to those offered by Hooke.
In too many ways, this stalemate between Newton and his critics was petty, but it turned finally on an important point. Newton's argument relied crucially on experimental evidence; Hooke and Huygens would not grant the weight of that evidence. This was just the lesson Galileo had hoped to teach earlier in the century. Now it was Newton's turn.
Alchemy and Heresy
In his nineteenth-century biography of Newton, David Brewster surprised his readers with an astonishing discovery. He revealed for the first time that Newton's papers included a vast collection of books, manuscripts, laboratory notebooks, recipes, and copied material on alchemy. How could “a mind of such power . . . stoop to be even the copyist of the most contemptible alchemical poetry,” Brewster asked. Beyond that he had little more to say about Newton the alchemist.
By the time Brewster wrote his biography, alchemy was a dead and unlamented endeavor, and the modern discipline of chemistry was moving forward at a rapid pace. In Newton's century the rift between alchemy and chemistry was just beginning to open, and in the previous century alchemy was chemistry.
Alchemists, like today's chemists, studied conversions of substances into other substances, and prescribed the rules and recipes that governed the changes. The ultimate conversion for the alchemists was the transmutation of metals, including the infamous transmutation of lead into gold. The theory of transmutation had many variations and refinements, but a fundamental part of the doctrine was the belief that metals are compounded of mercury and sulfur not ordinary mercury and sulfur but principles extracted from them, a “spirit of sulfur” and a “philosophic mercury.” The alchemist's goal was to extract these principles from impure natural mercury and sulfur; once in hand, the pure forms could be combined to achieve the desired transmutations. In the seventeenth century, this program was still plausible enough to attract practitioners, and the practitioners patrons, including kings.
The alchemical literature was formidable. There were hundreds of books (Newton had 138 of them in his library), and they were full of the bizarre terminology and cryptic instructions alchemists devised to protect their work from competitors. But Newton was convinced that with thorough and discriminating study, coupled with experimentation, he could mine a vein of reliable observations beneath all the pretense and subterfuge. So, in about 1669, he plunged into the world of alchemy, immediately enjoying the challenges of systematizing the chaotic alchemical literature and mastering the laboratory skills demanded by the alchemist's fussy recipes.
Newton's passion for alchemy lasted for almost thiry years. He accumulated more than a million words of manuscript material. An assistant, Humphrey Newton (no relation), reported that in the laboratory the alchemical experiments gave Newton “a great deal of satisfaction & Delight. . . . The Fire [in the laboratory furnaces] scarcely going out either Night or Day. . . . His Pains, his Dilligence at those sett times, made me think, he aim'd at something beyond ye Reach of humane Art & Industry.”
What did Newton learn during his years in company with the alchemists? His transmutation experiments did not succeed, but he did come to appreciate a fundamental lesson still taught by modern chemistry and physical chemistry: that the particles of chemical substances are affected by the forces of attraction and repulsion. He saw in some chemical phenomena a “principle of sociability” and in others “an endeavor to recede.” This was, as Westfall writes, “arguably the most advanced product of seventeenth-century chemistry.” It presaged the modern theory of “chemical affinities,” which will be addressed in chapter 10.
For Newton, the attraction forces he saw in his crucibles were of a piece with the gravitational force. There is no evidence that he equated the two kinds of forces, but some commentators have speculated that his concept of universal gravitation was inspired, not by a Lincolnshire apple, but by the much more complicated lessons of alchemy.
During the 1670s, Newton had another subject for continual study and thought; he was concerned with biblical texts instead of scientific texts. He became convinced that the early Scriptures expressed the Unitarian belief that although Christ was to be worshipped, he was subordinate to God. Newton cited historical evidence that this text was corrupted in the fourth century by the introduction of the doctrine of the Trinity. Any form of anti-Trinitarianism was considered heresy in the seventeenth century. To save his fellowship at Cambridge, Newton kept his unorthodox beliefs secret, and, as noted, he was rescued by a special dispensation when he could no longer avoid the ordination requirement of the fellowship.
Halley’s Question
In the fall of 1684, Edmond Halley, an accomplished astronomer, traveled to Cambridge with a question for Newton. Halley had concluded that the gravitational force between the Sun and the planets followed an inverse-square law that is, the connection between this “centripetal force” (as Newton later called it) and the distance r between the centers of the planet and the Sun is
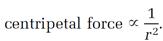
(Read “proportional to” for the symbol 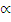 .) The force decreases by 1⁄22 = 1⁄4 if r doubles, by 1⁄32 = 1⁄9 if r triples, and so forth. Halley's visit and his question were later described by a Newton disciple, Abraham DeMoivre:
.) The force decreases by 1⁄22 = 1⁄4 if r doubles, by 1⁄32 = 1⁄9 if r triples, and so forth. Halley's visit and his question were later described by a Newton disciple, Abraham DeMoivre:
In 1684 Dr Halley came to visit [Newton] at Cambridge, after they had some time together, the Dr asked him what he thought the curve would be that would be described by the Planets supposing the force of attraction towards the Sun to be reciprocal to the square of their distance from it. Sr Isaac replied immediately that it would be an [ellipse], the Doctor struck with joy & amazement asked him how he knew it, why saith he I have calculated it, whereupon Dr Halley asked him for his calculation without farther delay, Sr Isaac looked among his papers but could not find it, but he promised him to renew it, & then send it to him.
A few months later Halley received the promised paper, a short, but remarkable, treatise, with the title De motu corporum in gyrum (On the Motion of Bodies in Orbit). It not only answered Halley’s question, but also sketched a new system of celestial mechanics, a theoretical basis for Kepler’s three laws of planetary motion.
Kepler’s Laws
Johannes Kepler belonged to Galileo's generation, although the two never met. In 1600, Kepler became an assistant to the great Danish astronomer Tycho Brahe,
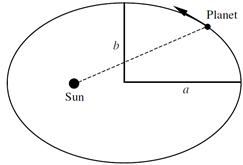
Figure 1.1. An elliptical planetary orbit. The orbit shown is exaggerated. Most planetary orbits are nearly circular.
and on Tycho's death, inherited both his job and his vast store of astronomical observations. From Tycho's data Kepler distilled three great empirical laws:
1. The Law of Orbits: The planets move in elliptical orbits, with the Sun situated at one focus.
Figure 1.1 displays the geometry of a planetary ellipse. Note the dimensions a and b of the semimajor and semiminor axes, and the Sun located at one focus.
2. The Law of Equal Areas: A line joining any planet to the Sun sweeps out equal areas in equal times.
Figure 1.2 illustrates this law, showing the radial lines joining a planet with the Sun, and areas swept out by the lines in equal times with the planet traveling different parts of its elliptical orbit. The two areas are equal, and the planet travels faster when it is closer to the Sun.
3. The Law of Periods: The square of the period of any planet about the Sun is proportional to the cube of the length of the semimajor axis.
A planet's period is the time it requires to travel its entire orbit 365 days for Earth. Stated as a proportionality, with P representing the period and a the length of the semimajor axis, this law asserts that
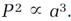
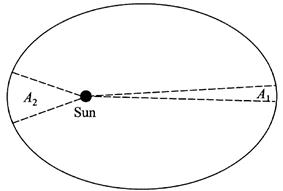
Figure 1.2. Kepler’s law of equal areas. The area A1 equals the area A2.
“I keep [a] subject constantly before me,” Newton once remarked, “and wait ’till the first dawnings open slowly, by little and little, into a full and clear light.” Kepler's laws had been on Newton's mind since his student days. In “first dawnings” he had found connections between the inverse-square force law and Kepler's first and third laws, and now in De motu he was glimpsing in “a full and clear light” the entire theoretical edifice that supported Kepler’s laws and other astronomical observations. Once more, Newton's work was “the passionate study of a man obsessed.” His principal theme was the mathematical theory of universal gravitation.
First, he revised and expanded De motu, still focusing on celestial mechanics, and then aimed for a grander goal, a general dynamics, including terrestrial as well as celestial phenomena. This went well beyond De motu, even in title. For the final work, Newton chose the Latin title Philosophiae naturalis principia mathematica (Mathematical Principles of Natural Philosophy), usually shortened to the Principia.
When it finally emerged, the Principia comprised an introduction and three books. The introduction contains definitions and Newton's candidates for the fundamental laws of motion. From these foundations, book 1 constructs extensive and sophisticated mathematical equipment, and applies it to objects moving without resistance for example, in a vacuum. Book 2 treats motion in resisting mediums for example, in a liquid. And book 3 presents Newton's cosmology, his “system of the world.”
In a sense, Halley deserves as much credit for bringing the Principia into the world as Newton does. His initial Cambridge visit reminded Newton of unfinished business in celestial mechanics and prompted the writing of De motu. When Halley saw De motu in November 1684, he recognized it for what it was, the beginning of a revolution in the science of mechanics. Without wasting any time, he returned to Cambridge with more encouragement. None was needed. Newton was now in full pursuit of the new dynamics. “From August 1684 until the spring of 1686,” Westfall writes, “[Newton's] life [was] a virtual blank except for the Principia.”
By April 1686, books 1 and 2 were completed, and Halley began a campaign for their publication by the Royal Society. Somehow (possibly with Halley exceeding his limited authority as clerk of the society), the members were persuaded at a general meeting and a resolution was passed, ordering “that Mr. Newton's Philosophiae naturalis principia mathematica be printed forthwith.” Halley was placed in charge of the publication.
Halley now had the Principia on the road to publication, but it was to be a bumpy ride. First, Hooke made trouble. He believed that he had discovered the inverse-square law of gravitation and wanted recognition from Newton. The acknowledgment, if any, would appear in book 3, now nearing completion. Newton refused to recognize Hooke's priority, and threatened to suppress book 3. Halley had not yet seen book 3, but he sensed that without it the Principia would be a body without a head. “Sr I must now again beg you, not to let your resentment run so high, as to deprive us of your third book,” he wrote to Newton. The beheading was averted, and Halley's diplomatic appeals may have been the decisive factor.
In addition to his editorial duties, Halley was also called upon to subsidize the publication of the Principia. The Royal Society was close to bankruptcy and unable even to pay Halley his clerk's salary of fifty pounds. In his youth, Halley had been wealthy, but by the 1680s he was supporting a family and his means were reduced. The Principia was a gamble, and it carried some heavy financial risks.
But finally, on July 5, 1687, Halley could write to Newton and announce that “I have at length brought your Book to an end.” The first edition sold out quickly. Halley at least recovered his costs, and more important, he received the acknowledgment from Newton that he deserved: “In the publication of this work the most acute and universally learned Mr Edmund Halley not only assisted me in correcting the errors of the press and preparing the geometrical figures, but it was through his solicitations that it came to be published.”
The Principia
What Halley coaxed from Newton is one of the greatest masterpieces in scientific literature. It is also one of the most inaccessible books ever written. Arguments in the Principia are presented formally as propositions with (sometimes sketchy) demonstrations. Some propositions are theorems and others are developed as illustrative calculations called “problems.” The reader must meet the challenge of each proposition in sequence to grasp the full argument.
Modern readers of the Principia are also burdened by Newton's singular mathematical style. Propositions are stated and demonstrated in the language of geometry, usually with reference to a figure. (In about five hundred pages, the Principia has 340 figures, some of them extremely complicated.) To us this seems an anachronism. By the 1680s, when the Principia was under way, Newton had already developed his fluxional method of calculus. Why did he not use calculus to express his dynamics, as we do today?
Partly it was an aesthetic choice. Newton preferred the geometry of the “ancients,” particularly Euclid and Appolonius, to the recently introduced algebra of Descartes, which played an essential role in fluxional equations. He found the geometrical method “much more elegant than that of Descartes . . . [who] attains the result by means of an algebraic calculus which, if one transcribed it in words (in accordance with the practice of the Ancients in their writings) is revealed to be boring and complicated to the point of provoking nausea, and not be understood.”
There was another problem. Newton could not use the fluxion language he had invented twenty years earlier for the practical reason that he had never published the work (and would not publish it for still another twenty years). As the science historian Francois De Gandt explains, “[The] innovative character [of the Principia] was sure to excite controversy. To combine with this innovative character another novelty, this time mathematical, and to make unpublished procedures in mathematics the foundation for astonishing physical assertions, was to risk gaining nothing.”
So Newton wrote the Principia in the ancient geometrical style, modified when necessary to represent continuous change. But he did not reach his audience. Only a few of Newton's contemporaries read the Principia with comprehension, and following generations chose to translate it into a more transparent, if less elegant, combination of algebra and the Newton-Leibniz calculus. The fate of the Principia, like that of some of the other masterpieces of scientific literature (Clausius on thermodynamics, Maxwell on the electromagnetic field, Boltzmann on gas theory, Gibbs on thermodynamics, and Einstein on general relativity), was to be more admired than read.
The fearsome challenge of the Principia lies in its detailed arguments. In outline, free of the complicated geometry and the maddening figures, the work is much more accessible. It begins with definitions of two of the most basic concepts of mechanics:
Definition 1: The quantity of matter is the measure of the same arising from its density and bulk conjointly.
Definition 2: The quantity of motion is the measure of the same, arising from the velocity and quantity of matter conjointly.
By “quantity of matter” Newton means what we call “mass,” “quantity of motion” in our terms is “momentum,” “bulk” can be measured as a volume, and “density” is the mass per unit volume (lead is more dense than water, and water more dense than air). Translated into algebraic language, the two definitions read
m = ρV, (12)
and
p = mv, (13)
in which mass is represented by m, density by ρ, volume by V, momentum by p, and velocity by v.
Following the definitions are Newton's axioms, his famous three laws of motion. The first is Galileo's law of inertia:
Law 1: Every body continues in its state of rest, or of uniform motion in a right [straight] line, unless it is compelled to change that state by forces impressed upon it.
The second law of motion has more to say about the force concept:
Law 2: The change of motion is proportional to the motive force impressed; and is made in the direction of the right line in which the force is impressed.
By “change of motion” Newton means the instantaneous rate of change in the momentum, equivalent to the time derivative dp/dt. In the modern convention, force is defined as this derivative, and the equation for calculating a force f is simply
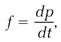 (14)
(14)
or, with the momentum p evaluated by equation (13),
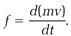 (15)
(15)
The first two laws convey simple physical messages. Imagine that your car is coasting on a flat road with the engine turned off. If the car meets no resistance (for example, in the form of frictional effects), Newton's first law tells us that the car will continue coasting with its original momentum and direction forever. With the engine turned on, and your foot on the accelerator, the car is driven by the engine's force, and Newton's second law asserts that the momentum increases at a rate (=dp/dt) equal to the force. In other words: increase the force by depressing the accelerator and the car's momentum increases.
Newton's third law asserts a necessary constraint on forces operating mutually between two bodies:
Law 3: To every action there is always opposed an equal reaction: or, the mutual actions of two bodies upon each other are always equal, and directed to contrary parts.
Newton's homely example reminds us, “If you press on a stone with your finger, the finger is also pressed by the stone.” If this were not the case, the stone would be soft and not stone like.
Building from this simple, comprehensible beginning, Newton takes us on a grand tour of terrestrial and celestial dynamics. In book 1 he assumes an inverse square centripetal force and derives Kepler's three laws. Along the way (in proposition 41), a broad concept that we now recognize as conservation of mechanical energy emerges, although Newton does not use the term “energy,” and does not emphasize the conservation theme.
Book 1 describes the motion of bodies (for example, planets) moving without resistance. In book 2, Newton approaches the more complicated problem of motion in a resisting medium. This book was something of an afterthought, originally intended as part of book 1. It is more specialized than the other two books, and less important in Newton's grand scheme.
Book 3 brings the Principia to its climax. Here Newton builds his “system of the world,” based on the three laws of motion, the mathematical methods developed earlier, mostly in book 1, and empirical raw material available in astronomical observations of the planets and their moons.
The first three propositions put the planets and their moons in elliptical orbits controlled by inverse-square centripetal forces, with the planets orbiting the Sun, and the moons their respective planets. These propositions define the centripetal forces mathematically but have nothing to say about their physical nature.
Proposition 4 takes that crucial step. It asserts “that the Moon gravitates towards the earth, and is always drawn from rectilinear [straight] motion, and held back in its orbit, by the force of gravity.” By the “force of gravity” Newton means the force that causes a rock (or apple) to fall on Earth. The proposition tells us that the Moon is a rock and that it, too, responds to the force of gravity.
Newton's demonstration of proposition 4 is a marvel of simplicity. First, from the observed dimensions of the Moon's orbit he concludes that to stay in its orbit the Moon falls toward Earth 15.009 “Paris feet” (= 16.000 of our feet) every second. Then, drawing on accurate pendulum data observed by Huygens, he calculates that the number of feet the Moon (or anything else) would fall in one second on the surface of Earth is 15.10 Paris feet. The two results are close enough to each other to demonstrate the proposition.
Proposition 5 simply assumes that what is true for Earth and the Moon is true for Jupiter and Saturn and their moons, and for the Sun and its planets.
Finally, in the next two propositions Newton enunciates his universal law of gravitation. I will omit some subtleties and details here and go straight to the algebraic equation that is equivalent to Newton's inverse-square calculation of the gravitational attraction force F between two objects whose masses are m1 and m2,
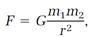 (16)
(16)
where r is the distance separating the centers of the two objects, and G, called the “gravitational constant,” is a universal constant. With a few exceptions, involving such bizarre objects as neutron stars and black holes, this equation applies to any two objects in the universe: planets, moons, comets, stars, and galaxies. The gravitational constant G is always given the same value; it is the hallmark of gravity theory. Later in our story, it will be joined by a few other universal constants, each with its own unique place in a major theory.
In the remaining propositions of book 3, Newton turns to more-detailed problems. He calculates the shape of Earth (the diameter at the equator is slightly larger than that at the poles), develops a theory of the tides, and shows how to use pendulum data to demonstrate variations in weight at different points on Earth. He also attempts to calculate the complexities of the Moon's orbit, but is not completely successful because his dynamics has an inescapable limitation: it easily treats the mutual interaction (gravitational or otherwise) of two bodies, but offers no exact solution to the problem of three or more bodies. The Moon's orbit is largely, but not entirely, determined by the Earth-Moon gravitational attraction. The full calculation is a “three-body” problem, including the slight effect of the Sun. In book 3, Newton develops an approximate method of calculation in which the Earth-Moon problem is first solved exactly and is then modified by including the “perturbing” effect of the Sun. The strategy is one of successive approximations. The calculations dictated by this “perturbation theory” are tedious, and Newton failed to carry them far enough to obtain good accuracy. He complained that the prospect of carrying the calculations to higher accuracy “made his head ache.”
Publication of the Principia brought more attention to Newton than to his book. There were only a few reviews, mostly anonymous and superficial. As De Gandt writes, “Philosophers and humanists of this era and later generations had the feeling that great marvels were contained in these pages; they were told that Newton revealed truth, and they believed it. . . . But the Principia still remained a sealed book.”
The Opticks
Newton as a young man skirmished with Hooke and others on the theory of colors and other aspects of optics. These polemics finally drove him into a silence of almost thirty years on the subject of optics, with the excuse that he did not want to be “engaged in Disputes about these Matters.” What persuaded him to break the silence and publish more of his earlier work on optics, as well as some remarkable speculations, may have been the death of his chief adversary, Hooke, in 1703. In any case, Newton published his other masterpiece, the Opticks, in 1704.
The Opticks and the Principia are contrasting companion pieces. The two books have different personalities, and may indeed reflect Newton's changing persona. The Principia was written in the academic seclusion of Cambridge, and the Opticks in the social and political environment Newton entered after moving to London. The Opticks is a more accessible book than the Principia. It is written in English, rather than in Latin, and does not burden the reader with difficult mathematical arguments. Not surprisingly, Newton's successors frequently mentioned the Opticks, but rarely the Principia.
In the Opticks, Newton presents both the experimental foundations, and an attempt to lay the theoretical foundations, of the science of optics. He describes experiments that demonstrate the main physical properties of light rays: their reflection, “degree of refrangibility” (the extent to which they are refracted), “inflexion” (diffraction), and interference.
The term “interference” was not in Newton’s vocabulary, but he describes interference effects in what are now called “Newton’s rings.” In the demonstration experiment, two slightly convex prisms are pressed together, with a thin layer of air between them; a striking pattern of colored concentric rings appears, surrounding points where the prisms touch.
Diffraction effects are demonstrated by admitting into a room a narrow beam of sunlight through a pinhole and observing that shadows cast by this light source on a screen have “Parallel Fringes or Bands of colour'd Light” at their edges.
To explain this catalogue of optical effects, Newton presents in the Opticks a theory based on the concept that light rays are the trajectories of small particles. As he puts it in one of the “queries” that conclude the Opticks: “Are not the Rays of Light very small Bodies emitted from shining Substances? For such Bodies will pass through Mediums in right Lines without bending into the Shadow, which is the Nature of the Rays of Light.”
In another query, Newton speculates that particles of light are affected by optical forces of some kind: “Do not Bodies act upon Light at a distance, and by their action bend its Rays; and is not this action strongest at the least distance?”
With particles and forces as the basic ingredients, Newton constructs in the Opticks an optical mechanics, which he had already sketched at the end of book 1 of the Principia. He explains reflection and refraction by assuming that optical forces are different in different media, and diffraction by assuming that light rays passing near an object are more strongly affected by the forces than those more remote.
To explain the rings, Newton introduces his theory of “fits,” based on the idea that light rays alternate between “Fits of easy Reflexion, and . . . Fits of easy Transmission.” In this way, he gives the rays periodicity, that is, wavelike character. However, he does not abandon the particle point of view, and thus arrives at a complicated duality.
We now understand Newton's rings as an interference phenomenon, arising when two trains of waves meet each other. This theory was proposed by Thomas Young, one of the first to see the advantages of a simple wave theory of light, almost a century after the Opticks was published. By the 1830s, Young in England and Augustin Fresnel in France had demonstrated that all of the physical properties of light known at the time could be explained easily by a wave theory.
Newton's particle theory of light did not survive this blow. For seventy-five years the particles were forgotten, until 1905, when, to everyone's astonishment, Albert Einstein brought them back. (But we are getting about two centuries beyond Newton's story. I will postpone until later an extended excursion into the strange world of light waves and particles.)
The queries that close the Opticks show us where Newton finally stood on two great physical concepts. In queries 17 through 24, he leaves us with a picture of the universal medium called the “ether,” which transmits optical and gravitational forces, carries light rays, and transports heat. Query 18 asks, “Is not this medium exceedingly more rare and subtile than the Air, and exceedingly more elastick and active? And doth not it readily pervade all Bodies? And is it not (by its elastick force) expanded through all the Heavens?” The ether concept in one form or another appealed to theoreticians through the eighteenth and nineteenth centuries. It met its demise in 1905, that fateful year when Einstein not only resurrected particles of light but also showed that the ether concept was simply unnecessary.
In query 31, Newton closes the Opticks with speculations on atomism, which he sees (and so do we) as one of the grandest of the unifying concepts in physics. He places atoms in the realm of another grand concept, that of forces: “Have not the small particles of Bodies certain Powers, Virtues or Forces, by which they act at a distance, not only upon the Rays of Light for reflecting, refracting, and inflecting them [as particles], but also upon one another for producing a great Part of the Phaenomena of Nature?”
He extracts, from his intimate knowledge of chemistry, evidence for attraction and repulsion forces among particles of all kinds of chemical substances, metals, salts, acids, solvents, oils, and vapors. He argues that the particles are kinetic and indestructible: “All these things being considered, it seems probable to me, that God in the Beginning form'd Matter in solid, massy, hard, impenetrable, moveable Particles, of such Sizes and Figures, and in such Proportion to Space, as most conduced to the End for which he form’d them; even so very hard, as never to wear or break in pieces; no ordinary Power being able to divide what God himself made one in the First Creation.”
London
There were two great divides in Newton's adult life: in the middle 1660s from the rural surroundings of Lincolnshire to the academic world of Cambridge, and thirty years later, when he was fifty-four, from the seclusion of Cambridge to the social and political existence of a well-placed civil servant in London. The move to London was probably inspired by a feeling that his rapidly growing fame deserved a more material reward than anything offered by the Lucasian Professorship. We can also surmise that he was guided by an awareness that his formidable talent for creative work in science was fading.
In March 1696, Newton left Cambridge, took up residence in London, and started a new career as warden of the Mint. The post was offered by Charles Montague, a former student and intimate friend who had recently become chancellor of the exchequer. Montague described the warden's office to Newton as a sinecure, noting that “it has not too much busnesse to require more attendance than you may spare.” But that was not what Newton had in mind; it was not in his character to perform any task, large or small, superficially.
Newton did what he always did when confronted with a complicated problem: he studied it. He bought books on economics, commerce, and finance, asked searching questions, and wrote volumes of notes. It was fortunate for England that he did. The master of the Mint, under whom the warden served, was Thomas Neale, a speculator with more interest in improving his own fortune than in coping with a monumental assignment then facing the Mint. The English currency, and with it the Treasury, were in crisis. Two kinds of coins were in circulation, those produced by hammering a metal blank against a die, and those made by special machinery that gave each coin a milled edge. The hammered coins were easily counterfeited and clipped, and thus worth less than milled coins of the same denomination. Naturally, the hammered coins were used and the milled coins hoarded.
An escape from this threatening problem, general recoinage, had already been mandated before Newton's arrival at the Mint. He quickly took up the challenge of the recoinage, although it was not one of his direct responsibilities as warden. As Westfall comments, “[Newton] was a born administrator, and the Mint felt the benefit of his presence.” By the end of 1696, less than a year after Newton went to the Mint, the crisis was under control. Montague did not hesitate to say later that, without Newton, the recoinage would have been impossible. In 1699 Neale died, and Newton, who was by then master in fact if not in name, succeeded him.
Newton's personality held many puzzles. One of the deepest was his attitude toward women. Apparently he never had a cordial relationship with his mother. Aside from a woman with whom he had a youthful infatuation and to whom he may have made a proposal of marriage, there was one other woman in Newton's life. She was Catherine Barton, the daughter of Newton's half-sister Hannah Smith. Her father, the Reverend Robert Barton, died in 1693, and sometime in the late 1690s she went to live with Newton in London. She was charming and beautiful and had many admirers, including Newton's patron, Charles Montague. She became Montague's mistress, no doubt with Newton's approval. The affair endured; when he died, Montague left her a generous income. She was also a friend of Jonathan Swift's, and he mentioned her frequently in his collection of letters, called Journal to Stella. Voltaire gossiped: “I thought . . . that Newton made his fortune by his merit. . . . No such thing. Isaac Newton had a very charming niece . . . who made a conquest of Minister Halifax [Montague]. Fluxions and gravitation would have been of no use without a pretty niece.” After Montague's death, Barton married John Conduitt, a wealthy man who had made his fortune in service to the British army. The marriage placed him conveniently (and he was aptly named) for another career: he became an early Newton biographer.
Newton the administrator was a vital influence in the rescue of two institutions from the brink of disaster. In 1703, long after the recoinage crisis at the Mint, he was elected to the presidency of the Royal Society. Like the Mint when Newton arrived, the society was desperately in need of energetic leadership. Since the early 1690s its presidents had been aristocrats who were little more than figureheads. Newton quickly changed that image. He introduced the practice of demonstrations at the meetings in the major fields of science (mathematics, mechanics, astronomy and optics, biology, botany, and chemistry), found the society a new home, and installed Halley as secretary, followed by other disciples. He restored the authority of the society, but he also used that authority to get his way in two infamous disputes.
On April 16, 1705, Queen Anne knighted Newton at Trinity College, Cambridge. The ceremony appears to have been politically inspired by Montague (Newton was then standing for Parliament), rather than being a recognition of Newton's scientific achievements. Political or not, the honor was the climactic point for Newton during his London years.
More Disputes
Newton was contentious, and his most persistent opponent was the equally contentious Robert Hooke. The Newton story is not complete without two more accounts of Newton in rancorous dispute. The first of these was a battle over astronomical data. John Flamsteed, the first Astronomer Royal, had a series of observations of the Moon, which Newton believed he needed to verify and refine his lunar perturbation theory. Flamsteed reluctantly supplied the requested observations, but Newton found the data inaccurate, and Flamsteed took offense at his critical remarks.
About ten years later, Newton was still not satisfied with his lunar theory and still in need of Flamsteed's Moon data. He was now president of the Royal Society, and with his usual impatience, took advantage of his position and attempted to force Flamsteed to publish a catalogue of the astronomical data. Flamsteed resisted. Newton obtained the backing of Prince George, Queen Anne's husband, and Flamsteed grudgingly went ahead with the catalogue.
The scope of the project was not defined. Flamsteed wanted to include with his own catalogue those of previous astronomers from Ptolemy to Hevelius, but Newton wanted just the data needed for his own calculations. Flamsteed stalled for several years, Prince George died, and as president of the Royal Society, Newton assumed dictatorial control over the Astronomer Royal's observations. Some of the data were published as Historia coelestis (History of the Heavens) in 1712, with Halley as the editor. Neither the publication nor its editor was acceptable to Flamsteed.
Newton had won a battle but not the war. Flamsteed's political fortunes rose, and Newton's declined, with the deaths of Queen Anne in 1714 and Montague in 1715. Flamsteed acquired the remaining copies of Historia coelestis, separated Halley's contributions, and “made a sacrifice of them to Heavenly Truth” (meaning that he burned them). He then returned to the project he had planned before Newton's interference, and had nearly finished it when he died in 1719. The task was completed by two former assistants and published as Historia coelestis britannica in 1725. As for Newton, he never did get all the data he wanted, and was finally defeated by the sheer difficulty of precise lunar calculations.
Another man who crossed Newton's path and found himself in an epic dispute was Gottfried Leibniz. This time the controversy concerned one of the most precious of a scientist's intellectual possessions: priority. Newton and Leibniz both claimed to be the inventors of calculus.
There would have been no dispute if Newton had published a treatise composed in 1666 on his fluxion method. He did not publish that, or indeed any other mathematical work, for another forty years. After 1676, however, Leibniz was at least partially aware of Newton’s work in mathematics. In that year, Newton wrote two letters to Leibniz, outlining his recent research in algebra and on fluxions. Leibniz developed the basic concepts of his calculus in 1675, and published a sketchy account restricted to differentiation in 1684 without mentioning Newton. For Newton, that publication and that omission were, as Westfall puts it, Leibniz's “original sin, which not even divine grace could justify.”
During the 1680s and 1690s, Leibniz developed his calculus further to include integration, Newton composed (but did not publish) his De quadratura (quadrature was an early term for integration), and John Wallis published a brief account of fluxions in volume 2 of his Algebra. In 1699, a former Newton protégé, Nicholas Fatio de Duillier, published a technical treatise, Lineae brevissimi (Line of Quickest Descent), in which he claimed that Newton was the first inventor, and Leibniz the second inventor, of calculus. A year later, in a review of Fatio's Lineae, Leibniz countered that his 1684 book was evidence of priority.
The dispute was now ignited. It was fueled by another Newton disciple, John Keill, who, in effect, accused Leibniz of plagiarism. Leibniz complained to the secretary of the Royal Society, Hans Sloane, about Keill's “impertinent accusations.” This gave Newton the opportunity as president of the society to appoint a committee to review the Keill and Leibniz claims. Not surprisingly, the committee found in Newton's favor, and the dispute escalated. Several attempts to bring Newton and Leibniz together did not succeed. Leibniz died in 1716; that cooled the debate, but did not extinguish it. Newtonians and Leibnizians confronted each other for at least five more years.
Nearer the Gods
Biographers and other commentators have never given us a consensus view of Newton's character. His contemporaries either saw him as all but divine or all but monstrous, and opinions depended a lot on whether the author was friend or foe. By the nineteenth century, hagiography had set in, and Newton as paragon emerged. In our time, the monster model seems to be returning.
On one assessment there should be no doubt: Newton was the greatest creative genius physics has ever seen. None of the other candidates for the superlative (Einstein, Maxwell, Boltzmann, Gibbs, and Feynman) has matched Newton's combined achievements as theoretician, experimentalist, and mathematician.
Newton was no exception to the rule that creative geniuses lead self-centered, eccentric lives. He was secretive, introverted, lacking a sense of humor, and prudish. He could not tolerate criticism, and could be mean and devious in the treatment of his critics. Throughout his life he was neurotic, and at least once succumbed to breakdown.
But he was no monster. He could be generous to colleagues, both junior and senior, and to destitute relatives. In disputes, he usually gave no worse than he received. He never married, but he was not a misogynist, as his fondness for Catherine Barton attests. He was reclusive in Cambridge, where he had little admiration for his fellow academics, but entertained well in the more stimulating intellectual environment of London.
If you were to become a time traveler and meet Newton on a trip back to the seventeenth century, you might find him something like the performer who first exasperates everyone in sight and then goes on stage and sings like an angel. The singing is extravagantly admired and the obnoxious behavior forgiven. Halley, who was as familiar as anyone with Newton's behavior, wrote in an ode to New ton prefacing the Principia that “nearer the gods no mortal can approach.” Albert Einstein, no doubt equal in stature to Newton as a theoretician (and no paragon), left this appreciation of Newton in a foreword to an edition of the Opticks:
Fortunate Newton, happy childhood of science! He who has time and tranquility can by reading this book live again the wonderful events which the great Newton experienced in his young days. Nature to him was an open book, whose letters he could read without effort. The conceptions which he used to reduce the material of experience to order seemed to flow spontaneously from experience itself, from the beautiful experiments which he ranged in order like playthings and describes with an affectionate wealth of details. In one person he combined the experimenter, the theorist, the mechanic and, not least, the artist in exposition. He stands before us strong, certain, and alone: his joy in creation and his minute precision are evident in every word and in every figure.
 الاكثر قراءة في علماء الفيزياء
الاكثر قراءة في علماء الفيزياء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


