Rudolf Clausius

Formulas and Conventions
To describe a system in the style of thermodynamics, one must first define the system's state with suitable state-determining variables such as the volume V and temperature t (t now stands for Celsius temperature). Small changes in V and t, brought on as the system is put through some process, are represented by dV and dt. These symbols can denote either increases or decreases, and that means dV and dt are implicitly either positive or negative. In an expansion, for example, the volume of the system increases, so the change dV is positive; in compression, the volume decreases and dV is negative. Similarly, positive dt describes a temperature increase, and negative dt a temperature decrease.
Heating and working are the fundamental processes of thermodynamics. As both Clausius and Thomson understood, they involve interactions between a system and its surroundings. For example, adding a small amount of heat dQ to a system from the surroundings is a small step in a heating process. Heat added to a system is counted as positive, and dQ is implicitly positive. The reverse process removes the heat dQ from the system, and dQ is negative. These conventions are illustrated in figure 1.1.
A working process might be the compression of a gas in a piston-cylinder device, as in a car engine. A small step in the compression process is represented by the small amount of work dW done on the system (the gas), and it is counted positive. In the reverse process, expansion, the system does work on its surroundings; this is work output and dW is negative. See figure 1.2. If we slowly add a small amount of heat dQ to a system, the response is likely to be a small temperature increase dt, accompanied by a small expansion expressed by the volume increase dV. The heat and its two effects are related by an equation that was an indispensable mathematical tool for Clausius,
dQ = MdV + Cdt. (1)
The coefficient C in this equation is called a “heat capacity.” We can isolate it by assuming that the volume is held constant, so there is no change in volume, dV = 0, and from equation (1),
dQ = Cdt (constant V). (2)
Suppose we add dQ = 0.1 heat units and measure the temperature change dt = 0.001oC. Then the heat capacity calculated with equation (2) is
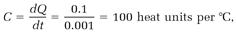
demonstrating that the heat capacity is the number of heat units required to raise the temperature of the system one degree.
If we compress a gaseous system and change its volume by dV, the small amount of work done dW is proportional to the volume change,
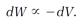 (3)
(3)
(Read “proportional to” for the symbol ∝.) The minus sign preceding dV is dictated by the sign conventions we have adopted for dW and dV. The compression
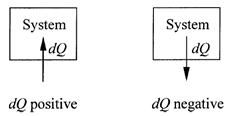
Figure 1.1. Illustration of the sign convention for dQ.
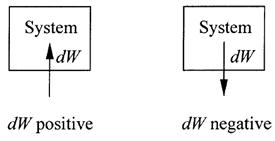
Figure 1.2. Illustration of the sign convention for dW.
provides work input, so dW is positive, but dV is negative because the compression decreases the volume. The mismatch of signs is repaired by replacing dV with -dV, which is positive. The same recipe applies to an expansion, with dV positive and -dV negative, matched by a negative dW for work output. The work done in compression is also proportional to a pressure factor, as one might expect, because it certainly requires less work to compress a gas at low pressure than at high pressure. If the compression is done slowly, that pressure factor is simply the pressure P of the gas. With that factor included, the proportionality (3) becomes the equation
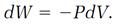 (4)
(4)
This equation is also valid for expansion of a gas, and even for expansion or compression of a liquid or solid.
Heat Transmitted and Converted
Clausius published a memoir in 1850 that reconciled Carnot's work with the discoveries of the intervening twenty-five years and formulated the first law of thermodynamics almost in its modern form. Clausius began his 1850 paper with a reference to the paper by Emile Clapeyron written two years after Carnot's death in the mathematical language understood then (and now) by theoreticians. For reasons he never had occasion to explain, Carnot had written his memoir in a mostly nonmathematical style that obscured his more subtle points.
Both Carnot and Clapeyron had been misled by the well-entrenched caloric theory of heat, which insisted that heat was indestructible, and could not therefore be converted to work in a heat engine or any other device. For them, the heat engine dropped the heat from a higher to a lower temperature without changing its amount. The time had come for Clausius, as about a year later it came for Thomson, to free the Carnot-Clapeyron work from the misconceptions of the caloric theory. Clausius did so by first making the fundamental assumption in his 1850 paper that part of the heat input to any heat engine is converted to work. The rest of the heat input is simply transmitted from a higher to a lower temperature, as in the Carnot-Clapeyron model, and it becomes the heat engine's output. In other words, heat can be affected by two kinds of transformations, transmission and conversion. Summarizing in an equation for one turn of a heat engine's cycle,
heat input = heat converted + heat transmitted, (5)
or
heat input - heat transmitted = heat converted. (6)
Clausius invoked a lengthy argument that put the last statement in the form of a complicated differential equation containing the two coefficients C and M.
The First Law
If Clausius had gone no further in his analysis, his 1850 paper would not have an important place in this history. The differential equation he had derived was mathematically valid, and its physical validity could be checked, but otherwise it had little significance beyond the immediate circumstances for which it was derived. Clausius was aware of these deficiencies, and his next effort was to reshape his argument into something more meaningful.
With some inspired mathematical manipulations, Clausius derived a second equation (equation [7] below) that proved a much more significant theoretical tool than his original equation. It can be found in any modern thermodynamics text as the standard mathematical version of the first law of thermodynamics. That two equations so closely related mathematically can differ so much in physical importance one equation little more than a historical curiosity, the other now known to any physicist, engineer, or chemist is vivid testimony that for the theoretical scientist, mathematics is a language whose message can be eloquent or dull, depending on how it is written and interpreted.
Clausius had only to integrate his original differential equation to reveal its physical message. He invoked a function of V and t, simply as a by-product of the integration, that was reminiscent of the false heat state function Q(V, t), except that this function really was a state function. The new function, which Clausius labeled U(V, t), was the first of a collection of valuable state functions that now dominate the practice of thermodynamics.
The quantity U was a proper state function, but what did it mean physically? Clausius answered by again making use of equation (1). With a few more mathematical strokes, he derived the equation
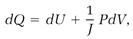 (7)
(7)
where P represents pressure, and the factor 1/J converts the mechanical units attached to the PdV term into the thermal units required for dQ.
Clausius had arrived here at the equation that modern students of thermodynamics have no difficulty recognizing as a mathematical statement of the first law of thermodynamics. In modern usage, no distinction is made between thermal and mechanical units, so the factor J is unnecessary, U is recognized as internal energy, and the equation is written so it evaluates changes in U,
dU = dQ - PdV. (8)
But in 1850, the energy concept was still unclear, and could not be part of Clausius's interpretation. Instead, he viewed equation (7) primarily as a contribution to the theory of heat. He understood dQ to measure the amount of heat added during a small step in a heating process. Once the heat entered the system, it could be “free” or “sensible” heat its effect could be measured on a thermometer or it could be converted to work. He recognized two kinds of work, that performed internally (against forces among molecules, in the modern interpretation) and that done externally, against an applied pressure in the surroundings. The term 1/J PdV in equation (7) evaluates the latter, so Clausius concluded that dU calculates two things: changes in the sensible heat (always an increase if heat is added) and the amount of internal work done, if any.
Clausius succinctly summarized his position in an appendix added to the 1850 paper in 1864, when he collected his papers in a book: “The function U, here introduced, is of great importance in the theory of heat; it will frequently come under discussion in the following memoirs. As stated, it involves two of the three quantities of heat, which enter into consideration when a body changes its condition; these are the augmentation of the so called sensible or actually present heat, and heat expended in interior work.”
At about the same time Clausius was developing this interpretation of his state function U(V, t), Thomson was inventing a theory based on an identical function, which he labeled e(V, t). Thomson had a name for his function “mechanical energy” and he understood it to be a measure of the mechanical effect (molecular kinetic and potential energy) stored in a system after it has exchanged heat and work with its surroundings. Thomson later called his function “intrinsic energy,” and still later Helmholtz supplied the name that has stuck, “internal energy.”
It is an impressive measure of the subtlety of the energy concept and of Thomson's insight that Clausius was not willing to accept Thomson's energy theory for fifteen years. Not until 1865 did he adopt Thomson's interpretation and begin calling his U function “energy.” He did not use Thomson’s or Helmholtz's terms.
In spite of his uncertainty about the physical meaning of the U function, Clausius had in his 1850 paper come close to a complete formulation of the first law of thermodynamics. Even the mathematical notation he used is that found in modern textbooks. Clifford Truesdell summarizes Clausius's achievements in the 1850 work: “There is no doubt that Clausius with his [1850] paper created classical thermodynamics. . . . Clausius exhibits here the quality of a great discoverer; to retain from his predecessors major and minor . . . what is sound while frankly discarding the rest, to unite previously disparate theories and by one simple if drastic change to construct a complete theory that is new yet firmly based upon previous successes.”
The “one simple if drastic change” made by Clausius was to assume that, in heat engines and elsewhere, heat could not only be dropped or transmitted from a higher to a lower temperature (as Carnot had assumed), but that it could also be converted into work. Others, particularly Joule, had recognized the possibility of heat-to-work conversions much of Joule's research was based on observations of the inverse conversion, work to heat but Clausius was the first to build the concept of such conversions into a general theory of heat.
Heat Transformations
Clausius had much more to add to his theoretical edifice based on the “simple if drastic change.” In 1854, he published a second paper on heat theory, which went well beyond the realm of the first law of thermodynamics and the concept of energy, and well into the new realm of the second law of thermodynamics and the concept of entropy. His initial assumption was again that heat could undergo two kinds of transformations. I will elaborate Clausius's terminology for the two transformations and call the dropping of heat from a high to a low temperature an instance of a “transmission transformation,” and the conversion of heat to work an example of a “conversion transformation.” Clausius was impressed that both kinds of transformations have two possible directions, one “natural” and the other “unnatural” (again, this is not Clausius’s terminology). In the natural direction, the transformation can proceed by itself, spontaneously and unaided, while the unnatural direction is not possible at all unless forced.
The natural direction for the conversion transformation can be seen in Joule's observations of heat production from work. Clausius saw the unnatural direction for the conversion transformation as the production of work from heat, a conversion that never takes place by itself, but always must be forced somehow in heat engine operation. The natural direction for the transmission transformation is the free conduction of heat from a high temperature to a low temperature. The unnatural direction is the opposite transport from a low temperature to a high temperature, which is impossible as a spontaneous process; such heat transport must be forced in a “heat pump,” like those used in air conditioners.
Clausius took this reasoning one significant step further. He saw that in heat engines the two kinds of heat transformations occur at the same time. In each cycle of heat engine operation, the transmission transformation takes place in its natural direction (heat dropped from a high to a low temperature), while the conversion transformation proceeds in its unnatural direction (heat converted to work). It is as if the transmission transformation were driving the conversion transformation in its unnatural direction.
Moreover, Clausius concluded, the two transformations are so nearly balanced that in reversible operations either can dominate the other. They are in some sense equivalent. Clausius set out to construct a quantitative “heat transformation theory” that could follow this lead. His goal was to assess “equivalence values” for both transformations in reversible, cyclic processes. He hoped that the equivalence values could then be used to express in a new natural law the condition of balance, or “compensation,” as he called it.
Although he could hardly have been aware of it at the time, Clausius had, in this simple theoretical expectation, started a line of reasoning as promising as any in the history of science. It would not be easy for him to appreciate fully the importance of what he was doing, but he now had all the theoretical clues he needed to reach the concept of entropy and its great principle, the second law of thermodynamics.
Clausius began his heat transformation theory with the axiom that heat is not transmitted spontaneously from a low temperature to a high temperature. (If you touch an icicle, heat passes from your warm hand to the cold icicle, and the icicle feels cold; icicles never feel warm.) In his 1854 paper, he stated the assumption: “Heat can never pass from a colder to a warmer body without some other change connected therewith occurring at the same time.” Later he simplified his axiom to: “Heat cannot of itself pass from a colder to a warmer body.”
The arguments Clausius used to develop his theory from this simple beginning are too lengthy to address here. Note that his equivalence values and condition of compensation revealed a fundamental pattern of heats and temperatures involved in any reversible, cyclic process. If ti is the temperature at which one step in such a process takes place, and if Qi is the heat input or output in that step, Clausius's corresponding equivalence value for the step is f (ti)Qi, where f (ti) is some universal function of the temperature ti. Summation of such terms for all the steps of a process, which we write with the notation Σf (ti )Qi (the symbol Σ denotes a summation), then evaluates the net equivalence value for the complete process. In Clausius's condition of compensation for reversible operation, the terms in the summation exactly cancel each other, and the result is
Σf (ti )Qi = 0 (reversible, cyclic operation).
For a process consisting of many small steps, each one involving a small heat transfer dQ at the temperature t, Clausius's compensation criterion is expressed as a summation over many small steps that is, as an integral
ʃf (t)dQ = 0 (reversible, cyclic process). (9)
For Clausius, this was a crucial result: it told him that he had found a new state function. To follow Clausius's reasoning here, we represent the new function temporarily with the generic symbol F (not the same as the F used earlier for Carnot's function), and define a small change dF with
dF = f (t)dQ (reversible process), (10)
so equation (9) becomes
ʃ dF = 0 (reversible, cyclic process). (11)
Clausius could now turn to a mathematical theorem that guarantees from this condition that F is a state function. Paralleling Clausius's other state function U(V, t), it could be identified as the function F(V, t).
At this point, Clausius had the underlying mathematical ingredients of his theory, but the physical interpretation of the mathematics was anything but clear. The physical meaning of the function U was still obscure, and the new function was even more of a mystery. As a skilled theorist, Clausius was aware of the dangers of attaching too much physical meaning to quantities that might be found later to be figments of the mathematical argument. He did not offer a name for the new state function in 1854, nor did he give it a symbol.
However, Clausius felt he could trust his conclusion that his compensation condition (11) did define a new state function, and from that mathematical fact he could determine the universal function f (t). A further mathematical argument led him to the conclusion that
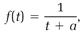 (12)
(12)
in which t + a defines absolute temperature on the ideal gas scale. Using T again to denote absolute temperature, Clausius's conclusion was that
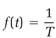
and this substituted in equation (10) completes the definition of Clausius's still nameless new thermodynamic state function,
 (13)
(13)
The Second Law
When he arrived at the mathematical equivalent of equation (13), Clausius must have been aware that he had made a promising beginning toward a broader theory. But the theory was still severely limited: for one thing, equation (13) applied only to reversible processes. The condition of reversibility had originally been invented by Carnot to define an ideal mode of heat engine operation, ideal in the sense that it gives maximum efficiency. Reversibility was essential in Clausius's argument leading to equation (13) because it enabled him to assert that the two kinds of heat transformations compensate each other.
Clausius had done great things with Carnot's theoretical style. One can imagine that if Carnot had lived longer he would have been fifty-four in 1850 and if he had recognized that heat can be transformed by conversion as well as by transmission, he would have reasoned much as Clausius did in 1850 and 1854. In the two papers, Clausius had done what Carnot demanded; and then in the 1854 paper, and later in 1865, he ventured beyond Carnot, into the realistic realm of irreversible processes, which were not of the ideal, reversible kind. Clausius's conclusion, as it is expressed by modern authors, is that for irreversible processes equation (13) is not valid, and instead it is replaced by an inequality,
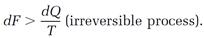 (14)
(14)
(Read “greater than” for the symbol >, and “less than” for <.)
Clausius had now brought forth two state functions, the function U and the dQ/T -related function we are temporarily labeling F. And he had generalized his theory so it was released from its earlier restrictions to reversible and cyclic processes. The paper in which he completed the generalization was published in 1865. By the time he wrote that paper, the last of his nine memoirs on thermodynamics, he was willing to accept the term “energy” for U, and he wrote equation (7) assuming no distinction between heat and mechanical units, so J = 1,
dQ = dU + PdV. (15)
Or, with dW = -PdV according to equation (4),
dQ = dU - dW. (16)
At long last (as it seems to us, with the benefit of hindsight), Clausius had enough confidence in his second state function to give it a name and a symbol. For no specified reason, he chose the letter S and wrote equation (13)
 (17)
(17)
and the inequality (14)
 (18)
(18)
(Clausius seems to have preferred letters from the last half of the alphabet; he used all the letters from M to Z, except for O, X, and Y, in his equations.) Because the function S calculated heat transformation equivalence values, he derived his word for it from the Greek word “trope,” meaning “transformation.” The word he proposed was “entropy,” with an “en-” prefix and a “-y” suffix to make the word a fitting partner for “energy.”
All this is familiar to the present-day student of thermodynamics, who continues the argument by deriving dQ = TdS from equation (17), substituting for dQ in equation (15) and rearranging to obtain
dU = TdS - PdV. (19)
We recognize this today as the master differential equation for the thermodynamic description of any system that is not changing chemically. Dozens of more specific equations can be derived from it.
Although Clausius was certainly aware of equation (19) and its mathematical power, he did not use it. He still had a curious ambivalence concerning his two state functions U and S. In a lengthy mathematical argument, he excised U and S from his equations (15) and (17), and in their place put functions of the heat Q and work W. It appears that Clausius hesitated because he hoped to give the energy U and entropy S molecular interpretations, but had not completed that program. The fundamental ingredients of this molecular picture were the kinetic and potential energy possessed by molecules, and in the determination of entropy, a macroscopic property he called “disgregation,” which measured “the degree in which the molecules of the [system] are dispersed.” For example, the disgregation for a gas (with the molecules widely separated) was larger than for a liquid or solid (with the molecules much closer to each other).
In the 1860s, molecular science was in its infancy, and these molecular interpretations could be no better than speculations. Clausius was well aware of this, and did not want to jeopardize the rest of his theory by building from molecular hypotheses. Rankine had done that and lost most of his audience. Nevertheless, Clausius did not want to discard the energy and entropy concepts completely. He found a safe middle ground where energy and entropy were “summarizing concepts,” as the science historian Martin Klein puts it, and the working equations of the theory were based strictly on the completely non-speculative concepts of heat and work. Clausius never finished his molecular interpretations, but his speculations, as far as they went, were sound. Even his disgregation theory was confirmed in the later work of Maxwell, Boltzmann, and Gibbs. Clausius's last words on thermodynamics, the last two lines of his 1865 paper, made readers aware of the grand importance of the two summarizing concepts, energy and entropy. He saw no reason why these concepts and their principles should be restricted to the earthbound problems of physics and engineering: they should have meaning for the entire universe of macroscopic phenomena. Stretching his scientific imagination to the limit, he pictured the universe with no thermal, mechanical, or other connections, so dQ = 0 and dW = 0, and then applied his statements (16) and (18) of the first and second laws of thermodynamics to this isolated system. According to equation (16), dU = 0 if dQ = 0 and dW = 0, so the energy of an isolated universe does not change: it is constant. With dQ = 0, the inequality (18) tells us that dS > 0, that is, all entropy changes are positive and therefore increasing. Presumably, no system, not even the universe, can change forever. When all change ceases, the increasing entropy reaches a maximum value. Clausius asked his readers to accept as “fundamental laws of the universe” his final verbal statements of the two laws of thermodynamics:
The energy of the universe is constant.
The entropy of the universe tends to a maximum.
 الاكثر قراءة في علماء الفيزياء
الاكثر قراءة في علماء الفيزياء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


