 المؤلف:
William Reusch
المؤلف:
William Reusch
 المصدر:
Virtual Textbook of Organic Chemistry
المصدر:
Virtual Textbook of Organic Chemistry
 الجزء والصفحة:
............
الجزء والصفحة:
............
 13-8-2018
13-8-2018
 2424
2424
A Model for NMR Spectroscopy
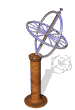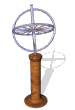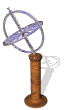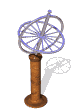
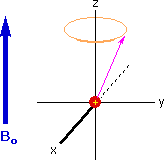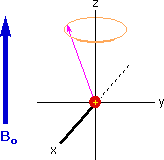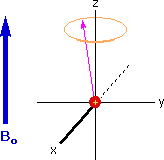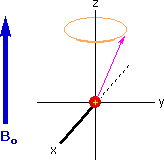
The model of a spinning nuclear magnet aligned with or against an external magnetic field (for I = 1/2 nuclei) must be refined for effective interpretation of nmr phenomena. Just as a spinning mass will precess in a gravitational field (a gyroscope), the magnetic moment μ associated with a spinning spherical charge will precess in an external magnetic field. In the following illustration, the spinning nucleus has been placed at the origin of a cartesian coordinate system, and the external field is oriented along the z-axis. The frequency of precession is proportional to the strength of the magnetic field, as noted by the equation: ωo = γBo. The frequency ωo is called the Larmor frequency and has units of radians per second. The proportionality constant γ is known as the gyromagnetic ratio and is proportional to the magnetic moment (γ = 2pm/hI).
 |
|
 |
magnetic moment
μ |
|
A Spinning Gyroscope
in a Gravity Field
|
|
A Spinning Charge
in a Magnetic Field
|
|
If rf energy having a frequency matching the Larmor frequency is introduced at a right angle to the external field (e.g. along the x-axis), the precessing nucleus will absorb energy and the magnetic moment will flip to its I = _1/2 state. This excitation is shown in the following diagram. Note that frequencies in radians per second may be converted to Hz (cps) by dividing by 2π.
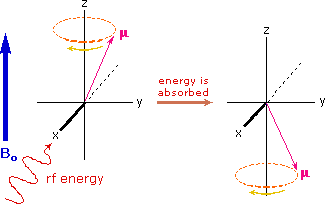
The energy difference between nuclear spin states is small compared with the average kinetic energy of room temperature samples, and the +1/2 and _1/2 states are nearly equally populated. Indeed, in a field of 2.34 T the excess population of the lower energy state is only six nuclei per million. Although this is a very small difference , when we consider the number of atoms in a practical sample (remember the size of Avogadro's number), the numerical excess in the lower energy state is sufficient for selective and sensitive spectroscopic measurements. The diagram on the left below illustrates the macroscopic magnetization of a sample containing large numbers of spin 1/2 nuclei at equilibrium in a strong external magnetic field (Bo). A slight excess of +1/2 spin states precess randomly in alignment with the external field and a smaller population of _1/2 spin states precess randomly in an opposite alignment. An overall net magnetization therefore lies along the z-axis.
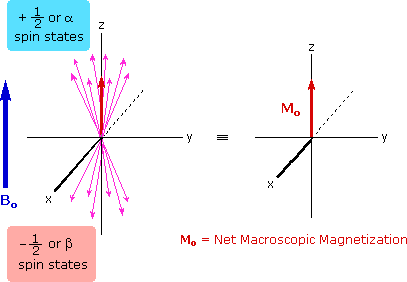

Net Macroscopic Magnetization of a Sample in an External Magnetic Field Bo Excitation by RF Energy and Subsequent Relaxation
The diagram and animation on the right show the changes in net macroscopic magnetization that occur as energy is introduced by rf irradiation at right angles to the external field. It is convenient to show the rf transmitter on the x-axis and the receiver-detector coil on the y-axis.
• First, the net magnetization shifts away from the z-axis and toward the y-axis. This occurs because some of the +1/2 nuclei are excited to the _1/2 state, and the precession about the z-axis becomes coherent (non-random), generating a significant y component to the net magnetization (M). The animation pauses at this stage.
• After irradiation the nuclear spins return to equilibrium in a process called relaxation. As the xy coherence disappears and the population of the +1/2 state increases, energy is released and detected by the receiver. The net magnetization spirals back, and eventually the equilibrium state is reestablished.
An inherent problem of the nmr experiment must be pointed out here. We have noted that the population difference between the spin states is proportionally very small. A fundamental requirement for absorption spectroscopy is a population imbalance between a lower energy ground state and a higher energy excited state. This can be expressed by the following equation, where A is a proportionality constant. If the mole fractions of the spin states are equal (η+ = η- ) then the population difference is zero and no absorption will occur. If the rf energy used in an nmr experiment is too high this saturation of the higher spin state will result and useful signals will disappear.
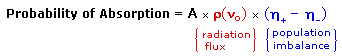
 الاكثر قراءة في التشخيص العضوي
الاكثر قراءة في التشخيص العضوي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


