Electrostatic Interactions
Electrostatic forces originate from the electric charges and dipoles of atoms and groups of atoms. They function inside macromolecules to maintain and to stabilize the molecular structure and to regulate the biological functions of catalysis and electron transfer. Electrostatic forces between molecules, facilitate specific molecular recognition and molecular assembly. The specific electrostatic field is determined by contributions from several factors, which originate from the intrinsic heterogeneity of biological macromolecules and from aqueous solvents.
1. Ionic Charges
In proteins, aspartic acid and glutamic acid residues have negatively ionizable side chains, and lysine, arginine, and histidine are positively ionizable. The amide and carboxyl termini of the polypeptide chain can also ionize, with, respectively, positive and negative charges. The intrinsic pK
a values of these groups in a normal aqueous environment are listed in Table 1. The actual pK
a value of a group in a folded protein can deviate from its intrinsic value, depending on the electrostatic field it experiences. The net charge of a protein is the sum of the positively and negatively ionized amino acid groups, plus any cofactor ions, and depends on the pH of the solvent. The pH at which a protein has no net charge is known as its isoelectric point. At neutral pH, most proteins are amphoteric, having both cationic and anionic groups at specific locations in the folded conformation.
Table 1. pK
a Values for Amino Acids in Peptides
a and Bases in Nucleosides
b
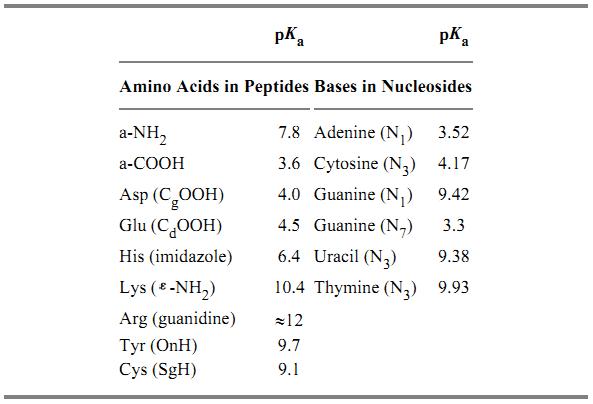 a
a Ref. 23.
b Ref. 24.
In nucleic acids, only the negative phosphate groups are charged at neutral pH, so nucleic acids do not show amphoteric properties. At very acidic or alkaline pH values, however, protonation or deprotonation of bases occurs, depending upon their pK
a values (Table 1. (
2. Permanent Electric Dipoles
A molecule or a group of atoms has a permanent electric dipole if it has an unequal electron distribution. This dipole spontaneously produces its own electric field, and the molecule or group is then described as polar. One of the more important polar groups in macromolecules is the peptide bond, which has a large dipole moment. The polar groups interact electrostatically with other polargroups in the same or other molecules or with polar solvent molecules or ions. Permanent dipoles within most macromolecules are small and are distributed in different orientations, except for the alpha-helix. It possesses a large permanent dipole moment due to the cooperatively aligned electric dipoles of the peptide bonds of the backbone (1(
3. Polarizability and Dielectric Constant
In an external electric field E, an electric dipole is induced even in a neutral, nonpolar molecule or group because the outer field modifies the electrostatic balance between the electrons and the nucleus in each atom. The magnitude of this dipole is given by m
induced = a
0E, where the coefficient a
0, the electronic polarizability, is proportional to the volume of the molecule or group. When the molecule or group also has additional permanent dipoles, they also reorient because of the external field. Consequently, the polarizability of a molecule is the sum of its electronic and orientational polarizabilities. The contribution from the orientational polarization of a polar group is generally much larger than that of the electronic polarization (2).
When a material is physicochemically homogeneous in a macroscopic volume, the dielectric constant of the material is related to the polarizability through the Clausius–Mossotti equation. Thus, the dielectric constant reflects the degree of polarizability of the material. A pure, polar liquid has a much larger dielectric constant than a nonpolar liquid. For example, the dielectric constants at 20 °C of water and cyclohexane are 80 and 2, respectively. The magnitude of the electrostatic interactions between charged groups or dipoles is relatively straightforward in such a homogeneous medium. It is inversely proportional to the distance between each pair of charges and to the dielectric constant of the medium. In contrast, proteins and nucleic acids are so heterogeneous, with polar and nonpolar groups distributed nonuniformly, that it is impossible to define an dielectric constant. Roughly speaking, however, the dielectric constant should be small in a hydrophobic core, perhaps 2 to 4, whereas the surface regions have larger values of 10 or larger (3. (
4. Electrostatic Shielding by Polar Solvents
When a charged, polar biological macromolecule is dissolved in a polar aqueous solvent, the solvent molecules rotate in response to their interaction with the solute macromolecule in an attempt to decrease the free energy of the entire system. Thus, the electrostatic force produced by the solute macromolecule is significantly shielded. This free energy is called the self-energy, the interaction of a solute charge or electric dipole with the dielectric environment (2). In addition, the density distribution of small ions in the solvent also changes to shield the electric field originating from the solute molecule. Small metal cations are located near the negative charges, and anions are near the positive point charges, as described by the Debye–Hückel approximation. Double-stranded DNA or RNA has a very high negative charge density of phosphate groups of the backbone, which is almost neutralized (about 88%) by condensed counterions, which are strongly restricted along the duplex, in addition to the Debye-Hückel type interaction. The density of the condensed counterions is relatively independent of the solvent conditions, but they are released from the polymer when the double helical conformation is deformed (4).
When the response to a given electric field is monitored directly, changes in the orientation and density distribution of the solvent molecules are the major responses to an external field. Therefore, passive measurement of the individual pKa values of the ionizable groups (5) and of the NMR chemical shift values of the nuclei (6) are good reporters of the local electrostatic field inside macromolecules. Both measurements are possible with the aid of multidimensional NMR techniques using stable isotope labeling (7). The charges and polarities of interest in proteins can be changed by site-directed mutagenesis, and the free energy difference associated with the electrostatic interaction can be evaluated (8).
5. Theoretical Approaches
Theoretical approaches to electrostatic interactions are divided between two types of theories: the macroscopic or continuum and the microscopic or molecular. In the continuum theory, the Poisson or Poisson–Boltzmann equation is solved for the solute–solvent system, assuming that the system is large enough to define its dielectric properties. Kirkwood first obtained an analytical solution for a simple spherical solute molecule embedded in a solvent with a high dielectric constant (9). With the aid of high-speed computational techniques, the exact shapes of biological macromolecules can be considered and the equations solved numerically (10). The computer program GRASP (11) is widely used to compute the electrostatic potential based on this method and to illustrate the electrostatic molecular surfaces of biological macromolecules and their assemblies, using red and blue colors for negative and positive charges, respectively. The drawbacks of the continuum theory (3) are (1) that the solute–solvent system is too heterogeneous to introduce the dielectric constant parameters and (2) that the calculations are based on static molecular conformations. Therefore, strict agreement between experiments and calculations is not expected. In the molecular theory, all of the atoms of the solute and solvent molecules are incorporated into the calculation, using the vacuum dielectric constant. Because the electric force is essentially long-range and the solvent molecules are significantly polar, reliable results are obtained only if the dynamics of the system are simulated for a sufficiently long period without simply cutting off the electrostatic forces.
6. Roles in Folded Conformations
Statistical analyses of the charge distributions on protein surfaces indicate that the charged groups are, on average, surrounded by charges of opposite sign and they tend to form ion pairs, which contribute to conformational stability (12, 13). The electrostatic contribution of ion pairs to protein stability is context-dependent, and the interaction energy of a single ion pair exposed to the solvent or even buried in the protein interior, varies experimentally from 0.5 to 5 kcal/mol. The entropic cost of forming rigid salt bridges is an opposing factor that reduces the free energy of the folded protein (14) . A cooperative salt-bridge network can contribute significantly to protein stability (15), as observed frequently on the surfaces of proteins of thermophilic origins. Acidic residues occur near the positive pole of the helical dipole at the N-terminus of an a-helix (12) and basic residues near the negative pole. They represent the helix caps (16). These interactions are not context-dependent, but only the first one or two turns of an a-helix give the essential contribution to protein stability by at most about 2 kcal/mol, independent of the length of the a-helix (17).
Unfavorable electrostatic interactions destabilize the folded conformation and are important in proteins. Unpaired buried charges and isolated hydrogen bonds are energetically expensive within the hydrophobic core because of the large self-energy. Thus, secondary structures, such as a-helices and beta-sheets, can usually be depicted in protein cores as simply the backbone structures because they do not leave any backbone hydrogen bond donors or acceptors unpaired (18).
The condensation of counterions contributes to the conformation and the stability of double helices of DNA and RNA, which are highly charged due to the ionized phosphate groups of the backbone. The ordered double-stranded conformation depends markedly on the ionic strength, and the melting temperature of the conformation is increased as ionic strength increases. Divalent cations interact with these duplexes more strongly than monovalent cations.
7. Enzyme Catalysis
Efficient enzyme catalysis is based on the decrease in the free energy of the transition state, and it is mediated by a well-designed active site structure and the electrostatic field. Protein engineering studies employing site-directed mutagenesis have highlighted the importance of ionizable or polar residues at the active site. In the catalytic reactions of proteins, the thiol group of cysteine residues, the hydroxyl group of serine or the imidazole group of histidine acts as a nucleophilic catalyst at the initial stage. Ionizable side chains can act as acid and base catalysts by giving and receiving a proton, respectively. Generally, when two ionizable groups are adjacent their pK
a values deviate greatly from the intrinsic values. One value becomes higher and the other becomes lower because of the strong coupling interaction between the two ionization states. Thus, even at a neutral pH, two such ionizable side chains can form acid and/or base catalysts, which are often observed to have unusual pK
a values at the active sites of enzymes. In addition, ligated metal ions play important roles in many examples of catalysis by correctly positioning the substrate molecules, by stabilizing the transition-state conformation, or by activating water molecules to form hydroxide ions.
The electron transfer reaction is an essential event in energy acquisition during respiration and photosynthesis. Several prosthetic groups in proteins, such as hemes, iron–sulfur clusters, and some transition metals, such as Cu, directly govern the reaction. The electron transfer reaction is finely controlled by the surrounding peptide chains of proteins through electrostatic interactions (19). In addition, because the prosthetic groups are often buried deeply in the protein, electrons are considered to transfer from the protein surface through certain, but not unique, paths in the protein molecule (20). Electrostatic interactions often trigger large-scale structural changes, especially when coupled to ATP and GTP hydrolysis. The ionic and polar interactions of proteins with the phosphate groups of ATP and GTP become reordered after their hydrolysis. This local phenomenon causes domain movement in multidomain proteins and results in large structural changes. Likewise, several allosteric transitions are considered to be mediated by salt bridges.
8. Molecular Recognition
Molecular recognition is a major focus of modern biology and biochemistry. Specific molecular recognition of individual biological macromolecules is involved in many biological phenomena. Protein–protein interactions are critical in biological signal transduction, and they guide the assembly of multimeric proteins, generally found in cell organelles, cytosol, and cell membranes. Protein molecular surfaces are involved in the recognition of other molecules. Hydrogen bonds and salt bridges often provide specificity, which is derived from the distinctive electrostatic complementarity between the molecular surfaces. At protein–protein interfaces, on average, 0.88 hydrogen bonds are found per 100 Å
2 of buried accessible surface area, and from 0 to 5 intersubunit salt bridges are observed between protein dimers (21).
Protein–nucleic acid interactions are the origin of complex genetic regulation. The backbone phosphate groups interact with the basic side chains of the protein, and specific base sequences are generally recognized through hydrogen bonds and hydrophobic interactions with the protein side chains (22). In the process of association, a basic protein approaches the DNA double helix by a long-range, electrostatic attractive force. Then the protein condenses, like a group of counterions, along the DNA duplex. Some of the condensed counterions are released. Then the protein slides along the double helix by one-dimensional diffusion, scanning the sequence, until it finally becomes positioned at the specific binding site. Specific basic residues in the protein molecule form ion pairs with the exposed phosphate groups of the DNA backbone. Thus, the local DNA backbone structure, which is completely neutralized, is deformed. In fact, the DNA structures bound by proteins are often deformed from the typical B-type conformation.
References
1. A. Wada (1976) Adv. Biophys. 9, 1–63.
2. J. N. Israelachvili (1985) Intermolecular and Surface Forces, Academic Press, London, Chaps. "4" and "5", pp. 36–64.
3. H. Nakamura, T. Sakamoto, and A. Wada (1988) Protein Eng. 2, 177–183.
4. M. T. Record Jr., J. H. Ha, and M. A. Fisher (1991) Methods Enzymol. 208, 291–343.
5. C. Tanford and R. Roxby (1972) Biochemistry 11, 2192–2198.
6. A. C. de Dios, J. G. Pearson, and E. Oldfield (1993) Science 260, 1491–1496.
7. Y. Oda et al. (1994) Biochemistry 33, 5275–5284.
8. L. Serrano et al. (1990) Biochemistry 29, 9434–9352.
9. J. G. Kirkwood (1934) J. Chem. Phys. 2, 351–361.
10. J. Warwicker and H. C. Watson (1982) J. Mol. Biol. 157, 671–679.
11. A. Nicholls, K. A. Sharp, and B. Honig (1991) Proteins 11, 281–296.
12. A. Wada and H. Nakamura (1981) Nature 293, 757–758.
13. D. J. Barlow and J. M. Thornton (1983) J. Mol. Biol. 168, 867–885.
14. S. Dao-pin, U. Sauer, H. Nicholson, and B. W. Matthews (1991) Biochemistry 30, 7142–7153.
15. A. Horovitz et al. (1990) J. Mol. Biol. 216, 1031–1044.
16. J. S. Richardson and D. C. Richardson (1988) Science 240, 1648–1652.
17. J. Åqvist, H. Luecke, F. A. Quiocho, and A. Warshel (1991) Proc. Natl. Acad. Sci. USA 88, 2026-2030.
18. A. V. Finkelstein and O. B. Ptitsyn (1987) Prog. Biophys. Molec. Biol. 50, 171–190.
19. T. Ichiye (1996) Structure 4, 1009–1012.
20. A. Kuki and P. G. Wolynes (1987) Science 236, 1647–1652.
21. S. Jones and J. M. Thornton (1995) Prog. Biophys. Molec. Biol. 63, 31–65.
22. C. O. Pabo and R. T. Sauer (1992) Ann. Rev. Biochem. 61, 1053–1095.
23. A. R. Fersht (1985) Enzyme Structure and Mechanism, 2nd ed., Freeman, New York, pp. 156, Table 5.1.
24. G. M. Blackburn (1996) in Nucleic Acids in Chemistry and Biology: DNA and RNA structure, 2nd ed. (G. M. Blackburn and M. J. Gait, eds.), Oxford University Press, Oxford, Chap. "2", p. 22, Table 2.2.

















