In homological algebra we consider sequences

· · · −→F   ^p→  G   ^q→  H   ^···→

where F, G, H etc. are modules over some unital ring R and p, q etc. are R-module homomorphisms. We denote the trivial module {0} by 0, and we denote by 0→G and G→0 the zero homomorphisms from 0 to G and from G to 0 respectively. (These zero homomorphisms are of course the only homomorphisms mapping out of and into the trivial module 0.)

Unless otherwise stated, all modules are considered to be left modules.

Definition Let R be a unital ring, let F, G and H be R-modules, and let p: F → G and q: G → H be R-module homomorphisms. The sequence F  ^p→G ^q→H of modules and homomorphisms is said to be exact at G if and only if image(p: F → G) = ker(q: G → H). A sequence of modules and homomorphisms is said to be exact if it is exact at each module occurring in the sequence (so that the image of each homomorphism is the kernel of the succeeding homomorphism).

A monomorphism is an injective homomorphism. An epimorphism is a surjective homomorphism. An isomorphism is a bijective homomorphism.

The following result follows directly from the relevant definitions.

Lemma 1.1 let R be a unital ring, and let h: G → H be a homomorphism of R-modules. Then

• h: G → H is a monomorphism if and only if 0→G  ^h→H is an exact sequence;

• h: G → H is an epimorphism if and only if G h →H→0 is an exact sequence;

• h: G → H is an isomorphism if and only if 0→G ^h→H →0 is an exact sequence.

Let R be a unital ring, and let F be a submodule of an R-module G.

Then the sequence

0→F  ⁱ→G   ^q→G/F→0,

is exact, where G/F is the quotient module, i: F ,→ G is the inclusion homomorphism,  and q: G → G/F is the quotient homomorphism. Conversely,  given any exact sequence of the form

0 →F  ⁱ →G ^q→H→0,

we can regard F as a submodule of G (on identifying F with i(F)), and then H is isomorphic to the quotient module G/F. Exact sequences of this type are referred to as short exact sequences.

We now introduce the concept of a commutative diagram. This is a diagram depicting a collection of homomorphisms between various modules occurring on the diagram. The diagram is said to commute if, whenever there are two routes through the diagram from a module G to a module H,  the homomorphism from G to H obtained by forming the composition of the homomorphisms along one route in the diagram agrees with that obtained by composing the homomorphisms along the other route. Thus, for example,  the diagram

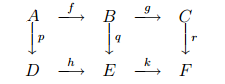
commutes if and only if q ◦ f = h ◦ p and r ◦ g = k ◦ q.

Proposition 1.2 Let R be a unital ring. Suppose that the following diagram of R-modules and R-module homomorphisms

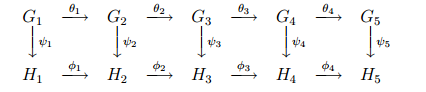
commutes and that both rows are exact sequences. Then the following results follow:

(i) if ψ₂ and ψ₄ are monomorphisms and if ψ₁ is a epimorphism then ψ₃ is an monomorphism,

(ii) if ψ₂ and ψ₄ are epimorphisms and if ψ₅ is a monomorphism then ψ₃ is an epimorphism.

Proof First we prove (i). Suppose that ψ₂ and ψ₄ are monomorphisms and that ψ₁ is an epimorphism. We wish to show that ψ₃ is a monomorphism.

Let x ∈ G₃ be such that ψ₃(x) = 0. Then ψ₄ (θ₃(x)) = φ₃ (ψ₃(x)) = 0,  and hence θ₃(x) = 0. But then x = θ₂(y) for some y ∈ G₂, by exactness.

Moreover

                                                φ₂ (ψ₂(y)) = ψ₃ (θ₂(y)) = ψ(x) = 0,

hence ψ₂(y) = φ₁(z) for some z ∈ H₁, by exactness. But z = ψ₁(w) for some w ∈ G₁, since ψ₁ is an epimorphism. Then

                                        ψ₂ (θ₁(w)) = φ₁ (ψ₁(w)) = ψ₂(y),

and hence θ₁(w) = y, since ψ₂ is a monomorphism. But then

                    x = θ₂(y) = θ₂ (θ₁(w)) = 0

by exactness. Thus ψ₃ is a monomorphism.

Next we prove (ii). Thus suppose that ψ₂ and ψ₄ are epimorphisms and that ψ₅ is a monomorphism. We wish to show that ψ₃ is an epimorphism.

Let a be an element of H₃. Then φ₃(a) = ψ₄(b) for some b ∈ G₄, since ψ₄ is an epimorphism. Now

                          ψ₅ (θ₄(b)) = φ₄ (ψ₄(b)) = φ₄ (φ₃(a)) = 0,

hence θ₄(b) = 0, since ψ5 is a monomorphism. Hence there exists c ∈ G₃ such that θ₃(c) = b, by exactness. Then

                              φ₃ (ψ₃(c)) = ψ₄ (θ₃(c)) = ψ₄(b),

hence φ₃ (a − ψ₃(c)) = 0, and thus a − ψ₃(c) = φ₂(d) for some d ∈ H₂, by exactness. But ψ₂ is an epimorphism, hence there exists e ∈ G₂ such that  ψ₂(e) = d. But then

                                ψ₃ (θ₂(e)) = φ₂ (ψ₂(e)) = a − ψ₃(c).

Hence a = ψ₃ (c + θ₂(e)), and thus a is in the image of ψ₃. This shows that ψ₃ is an epimorphism, as required.

The following result is an immediate corollary of Proposition 1.2.

Lemma 1.3 (Five-Lemma) Suppose that the rows of the commutative diagram of Proposition 1.2 are exact sequences and that ψ₁, ψ₂, ψ₄ and ψ₅ are isomorphisms. Then ψ₃ is also an isomorphism.