


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-5-2021
Date: 12-8-2021
Date: 29-7-2021
|
Let K be a simplicial complex. We introduce below boundary homomorphisms ∂q: Cq(K) → Cq−1(K) between the chain groups of K. If σ is an oriented q-simplex of K then ∂q(σ) is a (q − 1)-chain which is a formal sum of the (q − 1)-faces of σ, each with an orientation determined by the orientation of σ.
Let σ be a q-simplex with vertices v0, v1, . . . , vq. For each integer j between 0 and q we denote by hv0, . . . , vˆj, . . . , vqi the oriented (q − 1)-face 〈v0, . . . , vj−1, vj+1, . . . , vq〉
of the simplex σ obtained on omitting vj from the set of vertices of σ. In particular
〈vˆ0, v1, . . . , vq〉 ≡ 〈v1, . . . , vq〉, 〈v0, . . . , vq−1, vˆq〉 ≡ 〈v0, . . . , vq−1〉.
Similarly if j and k are integers between 0 and q, where j < k, we denote by
〈v0, . . . , vˆj , . . . , vˆk, . . . vq〉
the oriented (q−2)-face 〈v0, . . . , vj−1, vj+1, . . . , vk−1, vk+1, . . . , vq〉 of the simplex σ obtained on omitting vj and vk from the set of vertices of σ.
We now define a ‘boundary homomorphism’ ∂q: Cq(K) → Cq−1(K) for each integer q. Define ∂q = 0 if q ≤ 0 or q > dim K. (In this case one or other of the groups Cq(K) and Cq−1(K) is trivial.) Suppose then that 0 < q ≤ dim K. Given vertices v0, v1, . . . , vq spanning a simplex of K, let
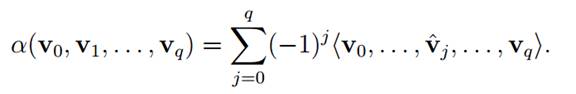
Inspection of this formula shows that α(v0, v1, . . . , vq) changes sign whenever two adjacent vertices vi−1 and vi are interchanged.
Suppose that vj = vk for some j and k satisfying j < k. Then
α(v0, v1, . . . , vq) = (−1)j〈v0, . . . , vˆj, . . . , vq〉 + (−1)k〈v0, . . . , vˆk, . . . , vq〉,
since the remaining terms in the expression defining α(v0, v1, . . . , vq) con tain both vj and vk. However (v0, . . . , vˆk, . . . , vq) can be transformed to (v0, . . . , vˆj, . . . , vq) by making k − j − 1 transpositions which interchange vj successively with the vertices vj+1, vj+2, . . . , vk−1. Therefore
〈v0, . . . , vˆk, . . . , vq〉= (−1)k−j−1〈v0, . . . , vˆj, . . . , vq〉.
Thus α(v0, v1, . . . , v=) = 0 unless v0, v1, . . . , vq are all distinct. It now follows immediately from Lemma 6.2 that there is a well-defined homomorphism ∂q: Cq(K) → Cq−1(K), characterized by the property that

whenever v0, v1, . . . , vq span a simplex of K.
Lemma 1.1 ∂q−1 ◦ ∂q = 0 for all integers q.
Proof The result is trivial if q < 2, since in this case ∂q−1 = 0. Suppose that q ≥ 2. Let v0, v1, . . . , vq be vertices spanning a simplex of K. Then

(since each term in this summation over j and k cancels with the corresponding term with j and k interchanged). The result now follows from the fact that the homomorphism ∂q−1 ◦ ∂q is determined by its values on all oriented q-simplices of K.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|