The mode of detection of lensing events depends on the telescope's angular resolution and its photometric sensitivity. When the two images can be resolved, as in the case discussed, the phenomenon is called a ‘macro lensing’ event. When the two images cannot be resolved, only the variability in the flux of the lensed source is observed. This is called a ‘microlensing’ event. Since θ_E increases with source distance behind the lens, there is a maximal source distance for microlensing, D_μ, which can be estimated by noting that the angular distance between the two images close to peak magnification is ∼2θ_E, and so

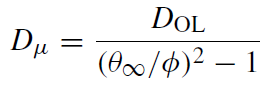 (1.1)

where φ is the telescope's angular resolution, θ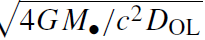_∞ ≡∼ 1.75'' is the Einstein angle for a source at infinity, and it is assumed that φ < θ_E is the criterion for resolving the two images.

The light curve for a constant velocity trajectory of a background source in the plane of the sky is given by substituting y(t),

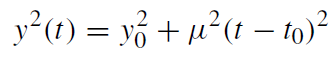 (9.25)

where y₀ is the impact parameter of the source trajectory relative to the lens, μ is the apparent motion, in units of θ_E per time, and t₀ is the time when y = y₀ (figure 1.1). The resulting light curve is symmetric about t₀, and achromatic (i.e. has the same shape in every wavelength). If the photometric sensitivity is large enough to detect the unlensed source, the event will appear as a flaring up of a persistent source; otherwise, it will appear as a transient flare.

In order to plan the observational strategy for detecting gravitational lensing, or to estimate how likely it is that an observed flare is due to lensing, it is necessary to calculate the detection probability. Two quantities are commonly used to express this probability, the optical depth and the lensing rate. The optical depth for gravitational lensing, τ , is usually defined in relation to the probability of having at least one lens along the line of sight. If the cross section of the lens at position zi is S(zi), and the number density of lenses there is n(zi), then the probability P of having at least one lens along the line of sight is the complement of the probability of not encountering any lens,

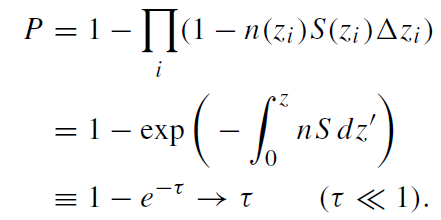 (1.3)

It should be emphasized that τ is not a probability, and that P and τ are interchangeable only when both are small. It is customary to define the lensing cross section as S = πθ²_E, which corresponds to the region where a source will be magnified by A > 1.34. This definition is useful when there are many possible lines of sight and it describes the probability that at any given instant a given line of sight will be lensed. This is relevant for Galactic microlensing searches, where millions of background stars are monitored

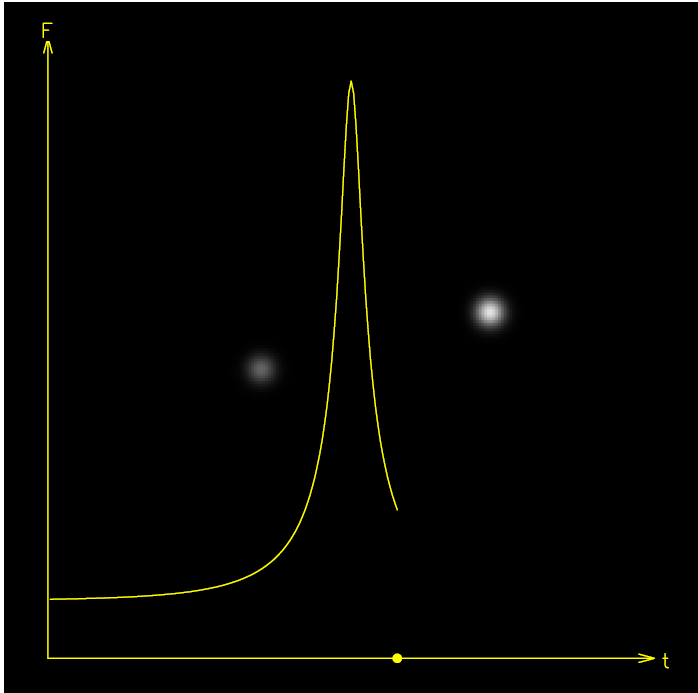
Figure 1.1. The microlensing light curve that corresponds to the lensing  to time         t = 19, in the case where the two images can not be resolved. The light curve is overlaid on the two lensed images as they would be observed if they could be resolved. The point on the time axis indicates the position of the source along its trajectory. The flux level on the left is the unmagnified flux of the source. The complete light curve will be symmetric relative to the peak flux.

simultaneously to find the rare one that is lensed by an intervening star. The observational situation for gravitational lensing by the MBH in the Galactic Center is different because the position of the lens is known and fixed, and so there is only one line of sight. In analogy to equation (1.3), the optical depth is then defined in relation to the probability of having at least one source behind the lens along the line of sight,

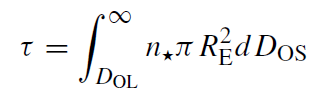 (1.4)

where R_E is the physical size of θ_E at the source plane,

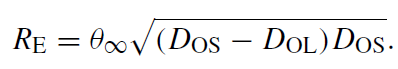 (1.5)

Rough estimates predict τ ∼ 1 for lensing by the MBH (assuming no limits on the photometric sensitivity).

The optical depth does not take into account the relative motions of the lens and source, which reshuffle their random alignment and introduces a timescale to the problem. A more useful quantity for the lensing by the MBH is the lensing event rate with flux above a detection threshold F₀ due to the motion of sources behind the MBH,

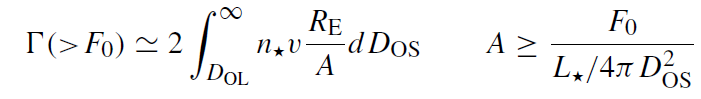 (1.6)

where v_* is the source star's projected velocity, L_* is its luminosity and A >> 1 is assumed. For practical applications, equation (1.6) has to be modified to take into account the range of stellar luminosities and velocities, dust extinction, the total duration of the observations T and the sampling rate ΔT (the mean duration of events magnified by more than A is t = π R_E/2Av; only events with ΔT < t < T can be detected).

The dependence of the lensing cross section, timescale and magnification on D_LS. The observational limitations, F₀, T and ΔT , place restrictions on D_LS and the impact parameter for which sources can be detected, and affect the typical timescales and peak magnification that are likely to be observed. For example, high magnification events typically have longer timescales because the source trajectory must have a smaller impact parameter and so it spends more time in the Einstein radius. Therefore, observations with limited temporal sampling will tend to pick out high magnification events. Were any microlensing events detected? A couple of possible transient flaring events were detected very close to Sgr A^* (Genzel et al 1997, Ghez et al 1998). For one of these a light curve was recorded, but as it was under-sampled only estimates of a timescale (∼1 yr) and a typical magnification (∼A > 5) could be derived from it. The a posteriori probability of detecting a lensing event was estimated at only 0.5%, but on the other hand, the observed timescale and magnification are close to the median value that is expected for the observational limitations (Alexander and Sternberg 1999). The interpretation of this event remains inconclusive.