


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 25-7-2016
Date: 14-8-2016
Date: 11-8-2016
|
Particle in Expanding Box
A particle of mass m is contained in a one-dimensional impenetrable box extending from x = -L/2 to x = +L/2. The particle is in its ground state.
a) Find the eigenfunctions of the ground state and the first excited state.
b) The walls of the box are moved outward instantaneously to form a box extending from –L ≤ x ≤ L. Calculate the probability that the particle will stay in the ground state during this sudden expansion.
c) Calculate the probability that the particle jumps from the initial ground state to the first excited final state.
SOLUTION
a) For a particle confined to a box –L/2 ≤ x ≤ L/2, the ground state ѱ0(x) and the first excited state ѱ1(x) are
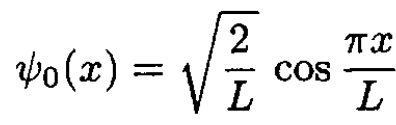 (1)
(1)
 (2)
(2)
After the sudden transition L → 2L, the final eigenfunctions are
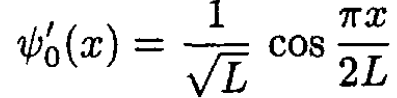 (3)
(3)
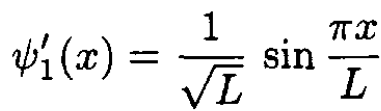 (4)
(4)
b) In the sudden approximation let P0j denote the probability that the particle starts in the ground state 0 and ends in the final state j:
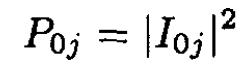 (5)
(5)
where the amplitude of the transition I0j is given by
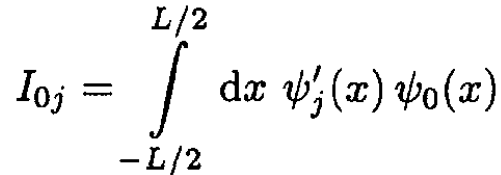 (6)
(6)
The amplitude for the particle to remain in its ground state is then
 (7)
(7)
The probability P00 is given by
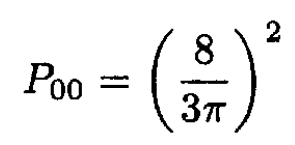 (8)
(8)
The same calculation for the transition between the initial ground state and final excited state ѱ'1 is as follows:
 (9)
(9)
where
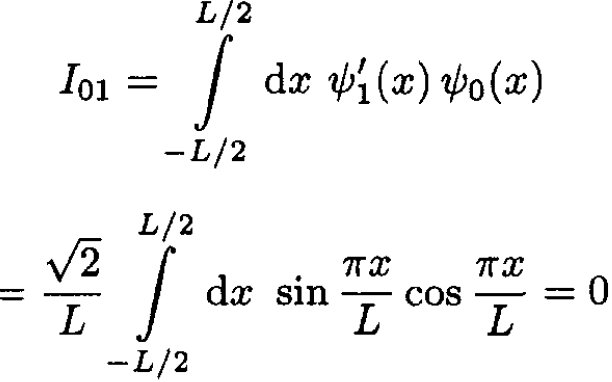 (10)
(10)
The integral is zero by parity, since the integrand is an odd function of x, so
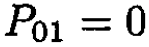 (11)
(11)



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|