


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 25-8-2016
Date: 8-8-2016
Date: 8-8-2016
|
Charged Particle in Uniform Magnetic Field
A nonrelativistic charged particle is orbiting in a uniform magnetic field of strength H0 at the center of a large solenoid. The radius of the orbit is R0. The field is changed slowly to H1. What is the new radius R1 of the orbit? If the field is suddenly changed back to H2 what is the final radius R2?
SOLUTION
Where we considered the adiabatic invariant for a mechanical system. Here, we have for the motion in the plane perpendicular to the magnetic field
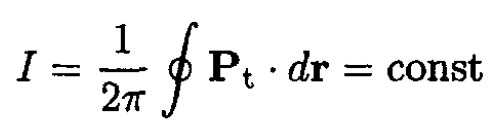
where
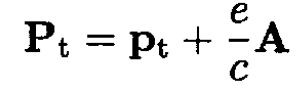
is the projection of the generalized momentum on this plane, and the integral is taken over one period of motion in this plane, whose shape is a circle. (A is the vector potential and is the charge of the particle.)
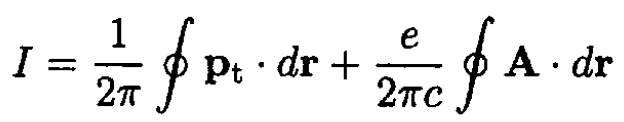 (1)
(1)
Using Stokes’ theorem and substituting  we obtain
we obtain
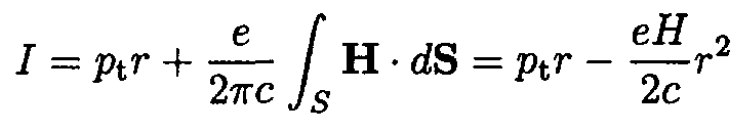 (2)
(2)
We used the fact that the absolute value of pt is constant. The minus sign before the second term occurs since the line integral about the orbit is opposite to the velocity of the charge. After substituting pt = eHr /c into (2), we obtain
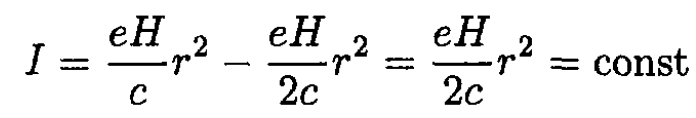 (3)
(3)
So, for a slow change of magnetic field from H0 to H1, we find
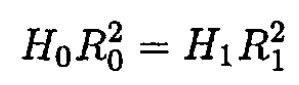
or

Now, if the field changes suddenly from H1 back to H0, then the energy ε is conserved
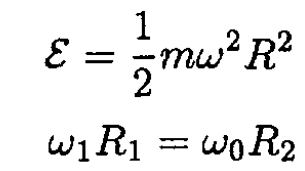
where ω1 and ω0 are cyclotron frequencies, corresponding to magnetic fields H1 and H0, respectively:
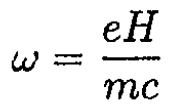
where m is the mass of the particle. Therefore,
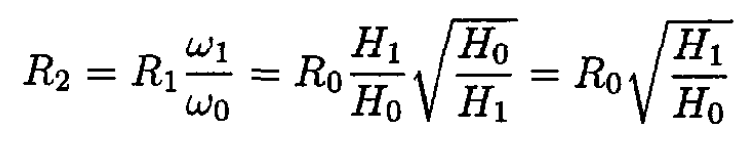



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|