Chromatic polynomials, developed by Birkhoff in the early 1900s as he studied the Four Color Problem, provide us with a method of counting the number of different colorings of a graph.

Before we introduce the polynomials, we should clarify what we mean by different colorings. Given a graph G, suppose that its vertices are labeled v₁, v₂, ... v_n. A coloring of G is an assignment of colors to these vertices, and we call two colorings C₁ and C₂ different if at least one vi receives a different color in C₁ than it does in C₂. For instance, the two colorings of K₄ shown in Figure 1.1 are considered different, since v₃ and v₄ receive different colorings.

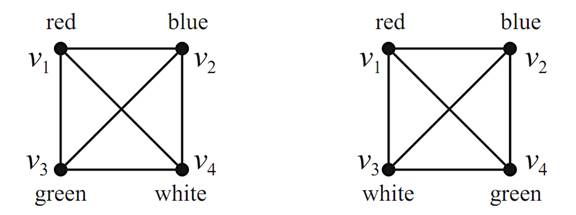
                               FIGURE 1.1. Two different colorings.

If we restrict ourselves to four colors, how many different colorings are there of K₄? Since there are four choices for v₁, then three for v₂,etc.,weseethat there are 4 · 3 · 2 · 1 different colorings of K₄ using four colors. If six colors were available, there would be 6 · 5 · 4 · 3 different colorings. If only two were available,  there would be no proper colorings of K₄.

In general, define c_G(k) to be the number of different colorings of a graph G using at most k colors. So we have c_K4 (4) = 24, c_K4 (6) = 360,and c_K4 (2) = 0.

In fact, if k and n are positive integers where k ≥ n, then

Further, if k<n, then c_Kn(k)=0. We also note that c_En(k)= k_n for all positive integers k and n. A simple but important property of c_G(k) is that G is k-colorable if and only if c_G(k) > 0. Equivalently, c_G(k) > 0 if and only if χ(G) ≤ k. Finding values of c_G(k) is relatively easy for some well-known graphs. Computing this function in general, though, can be hard. Birkhoff and Lewis [2] developed a way to reduce this hard problem to an easier one. Before we see their method, we need a definition.

        Let G be a graph and let e be an edge of G. Recall that G−e denotes the graph where e is removed from G. Define the graph G/e to be the graph obtained from G by removing e, identifying the end vertices of e, and leaving only one copy of any resulting multiple edges.

As an example, a graph G and the graphs G − bc and G/bc are shown in Figure 1.2.

Theorem 1.1. Let G be a graph and e be any edge of G. Then

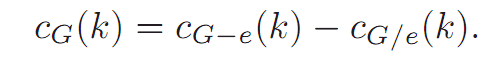
Proof. Suppose that the end vertices of e are u and v, and consider the graph G − e.

How many k-colorings are there of G−e where u and v are assigned the same color? If C is a such a coloring of G−e, then C can be thought of as a coloring of G/e, since u and v are colored the same. Similarly, any coloring of G/e can also be thought of as a coloring of G − e where u and v are colored the same. Thus,  the answer to this question is c_G/e(k).

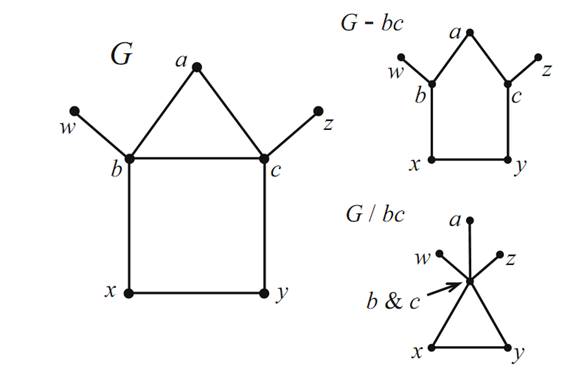
                           FIGURE 1.1. Examples of the operations.

Now, how many k-colorings are there of G − e where u and v are assigned different colors? If C is a such a coloring of G−e, then C can be considered as a coloring of G, since u and v are colored differently. Similarly, any coloring of G can also be thought of as a coloring of G−e where u and v are colored differently.

Thus, the answer to this second question is c_G(k).

Thus, the total number of k-colorings of G − e is

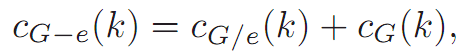
and the result follows.

For example, suppose we want to find cP4 (k). That is, howmany ways are there to color the vertices of P₄ with k colors available? We label the edges of P₄ as shown in Figure 1.2.

                                                                            FIGURE 1.2. The labeled edges of P₄.

The theorem implies that

For convenience, let us denote P₄ − e₁ and P₄/e₁ by G₁₁ and G₁₂, respectively (see Figure 1.3).

                                              FIGURE 1.3. The first application.

Applying the theorem again, we obtain

Denote the graphs G₁₁ − e₂, G₁₁/e₂, G₁₂ − e₂,and G₁₂/e₂ by G₂₁, G₂₂, G₂₃, and G₂₄, respectively (see Figure 1.4).

                                                                FIGURE 1.4. The second application.

Applying the theorem once more yields

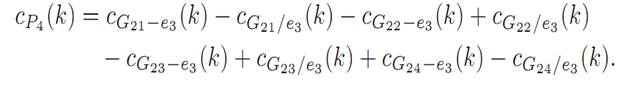
That is,

Thus

We should check a couple of examples. How many colorings of P₄ are there with one color?

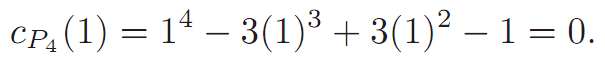
This, of course, makes sense. And how many colorings are there with two colors?

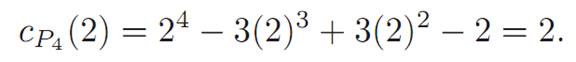
Figure 1.5 shows these two colorings. Score one for Birkhoff!

                              FIGURE 1.5. Two 2-colorings of P₄.

As you can see, chromatic polynomials provide a way to count colorings, and the Birkhoff–Lewis theorem allows you to reduce a problem to a slightly simpler one. We should note that it is not always necessary to work all the way down to empty graphs, as we did in the previous example. Once a graph G is obtained for which the value of c_G(k) is known, there is no need to reduce that one further.

We now present some properties of c_G(k).

Theorem 1.2. Let G be a graph of order n. Then

        1. c_G(k) is a polynomial in k of degree n,

        2. the leading coefficient of c_G(k) is 1,

        3. the constant term of c_G(k) is 0,

        4. the coefficients of c_G(k) alternate in sign, and

        5. the absolute value of the coefficient of the kn−1 term is the number of edges in G.

One proof strategy is to induct on the number of edges in G and use the Birkhoff–Lewis reduction theorem (Theorem 1.1). Before leaving this section, we should note that Birkhoff considered chromatic polynomials of planar graphs, and he hoped to find one of them that had 4 as aroot. If he had found  one, then the corresponding planar graph would not be 4-colorable, and hence would be a counterexample to the Four Color Conjecture. Although he was  unsuccessful in proving the Four Color Theorem, he still de-serves credit for producing a very nice counting technique.

_________________________________________________________________________________

1-Combinatorics and Graph Theory, Second Edition, John M. Harris • Jeffry L. Hirst • Michael J. Mossinghoff,2000,page(97-101)

2-G. D. Birkhoff and D. C. Lewis, Chromatic polynomials, Trans. Amer. Math. Soc. 60 (1946),no. 3, 355–451.