


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-5-2022
Date: 6-3-2022
Date: 28-2-2022
|
Which graphs embed in the plane? We have proved that K5 and K3,3 donot. In fact, these are the crucial graphs and lead to a characterization of planar graphs known as Kuratowski's Theorem. Kasimir Kuratowski once asked Frank Harary about the origin of the notation for K5 and K3,3. Harary replied, '''The K in K5 stands for Kasimir, and the K in K3,3 stands for Kuratowski!" Recall that a subdivision of a graph is a graph obtained from it by replacing edges with pairwise internally-disjoint paths
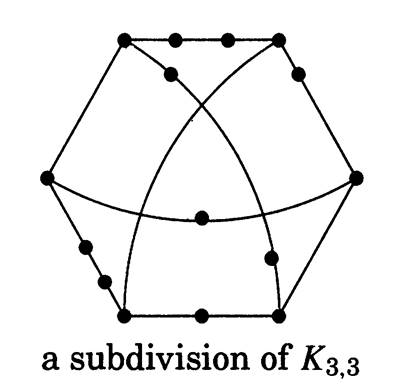
Theorem 1.1.
A graph is bipartite if and only if it contains no odd cycle.
Proof (outline). The proof of the necessary condition is easy when reasoning by the absurd and, in relation to the classes of the bipartition, following in order the vertices of an odd cycle. The proof of the sufficient condition isless simple but can be done in a constructive way, that is by producing the adequate bipartition. The principle is as follows: mark a first arbitrarily chosen vertex 0, then mark its neighbors 1, then take each of the newly marked vertices and mark their not-yet-marked neighbors 0, and so on until all vertices reached are marked 0 or 1. The crucial point is that if during this marking process two neighboring vertices happen to receive the same mark (twice 0 or twice 1) then there is an odd cycle in the graph. This can be seen by considering the paths defined by the succession of marked vertices which come to these two vertices and the edge joining them. With the hypothesis of the sufficient condition, this circumstance of two neighboring vertices bearing the same mark will not occur. The marks given to the vertices will define a bipartition in compliance with the definition of bipartite graphs. Any vertex will be marked as soon as the graph is connected, otherwise we should proceed independently with each connected component.
1-Graph Theory and Applications ,Jean-Claude Fournier, WILEY, page(37-38)
2- Introduction to Graph Theory Second Edition, Douglas B. West , Indian Reprint, 2002,page(246)



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|