


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 2-1-2021
Date: 6-2-2021
Date: 11-11-2020
|
SUM AND DIFFERENCE OPTICAL MIXING
So far we have examined primarily the phenomenon of second-harmonic generation, in which two identical incident waves (⍵1 and ⍵2 in our case) are mixed to produce a shorter wavelength (doubled frequency) result. In general, though, nonlinear processes extend much further, to the production of both sum and difference frequencies between source beams of different frequencies. It is well known that when two electromagnetic waves of different frequencies are mixed together, additional sum and difference frequencies are generated. In the world of electronics, this process of mixing is used in all radio receivers to generate intermediate frequencies, which are then detected. In AM radio receivers, incoming radio signals are mixed with a variable oscillator to produce a difference signal centered at 455 kHz. In FM receivers an intermediate frequency of 10.7 MHz is used. This scheme, called super heterodyning, allows the tuning of the receiver to any frequency desired by tuning an oscillator. The block diagram of an AM radio in Figure 1.1 shows how mixing works.
The same mixing effect can be accomplished with light by mixing it in a nonlinear crystal; in fact, most nonlinear optical effects have similar analogies in the world of electronics. In the effect described here, when two beams with frequencies ⍵1 and ⍵2 interact in a nonlinear crystal, they induce a polarization oscillating at ⍵1+ ⍵2 and ⍵1 -⍵2: in other words, a sum and a difference signal. To understand the mixing process, consider a model in which two beams with crests and valleys interact in a nonlinear crystal. Where crests for the two incident beams meet, the electric field strength is maximum and corresponds to the crests of two new

Figure 1.1. Mixing in a radio receiver.
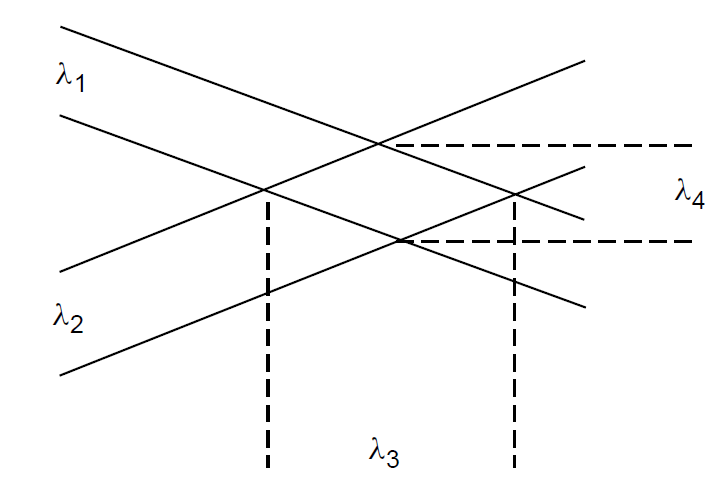
Figure 1.2. Model for mixing in a nonlinear crystal.
beams produced in the interaction. This interaction is depicted in Figure 1.2. Where λ1 and λ2 interact they can sum together to produce λ4 or a difference in λ3 . Remember that energies of these waves add and subtract so that the shorter wavelength sum (λ4) contains the sum of energies in photons λ1 and λ2 . Although laser beams are generally used for nonlinear mixing, intense incoherent sources can be used as well: Lasers simply offer a convenient source of intense light.
In terms of quantum mechanics, each incident photon is annihilated to produce a new photon that contains the total energy of the two individual incident photons. This is simple conservation of energy. Since frequency is proportional to energy, the frequency of the new photon is the sum of the frequencies of each incident photon.
Example 1.1 Up-Converted Frequency The process of mixing optical waves by a process such as that described in this section can be used to up-convert frequencies. One application involves the mixing of 10.6-μm radiation from a carbon dioxide laser with the 1.06-μm radiation from a YAG laser in a proustite crystal (one of the few nonlinear materials that is transparent at both wavelengths). The wavelength of the resulting radiation may be found by summing the frequency of each laser (2.83 × 1013 and 2.83 × 1014 Hz, respectively) to yield the summed component at 3.11 × 1014 Hz or 963 nm.
In addition to their value in mixing two frequencies, nonlinear processes may be used to mix three or more laser frequencies in a process called n-wave mixing. Such processes usually exhibit low efficiencies, however, and so are often restricted to the laboratory.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
مؤسسة السجناء السياسيين: سجلنا 120 ألفًا من ضحايا السجون والاعتقالات في عهد النظام السابق
|
|
|