The Sumerians and Babylonians, who inhabited present-day Syria, Jordan and Iraq around 4000 years ago, used a place-value system for their practical everyday use. We call it a place-value system because you can tell the ‘number’ by the positioning of a symbol. They also used 60 as the basic unit – what we call today a ‘base 60’ system. Vestiges of base 60 are still with us: 60 seconds in a minute, 60 minutes in an hour. When measuring angles we still reckon the full angle to be 360 degrees, despite the attempt of the metric system to make it 400 grads (so that each right angle is equal to 100 grads).

While our ancient ancestors primarily wanted numbers for practical ends, there is some evidence that these early cultures were intrigued by mathematics itself, and they took time off from the practicalities of life to explore them. These explorations included what we might call ‘algebra’ and also the properties of geometrical figures.

The Egyptian system from the 13th century BC used base ten with a system of hieroglyphic signs. Notably the Egyptians developed a system for dealing with fractions, but today’s place-value decimal notation came from the Babylonians, later refined by the Hindus. Where it has the advantage is the way it can be used to express both very small and very large numbers. Using only the Hindu-Arabic numerals 1, 2, 3, 4, 5, 6, 7, 8 and 9, computations can be made with relative ease. To see this let’s look at the Roman system. It suited their needs but only specialists in the system were capable of performing calculations with it.

The Roman system

The basic symbols used by the Romans were the ‘tens’ (I, X, C and M), and the ‘halves’ of these (V, L and D). The symbols are combined to form others. It has been suggested that the use of I, II, III and IIII derives from the appearance of our fingers, V from the shape of the hand, and by inverting it and joining the two together to form the X we get two hands or ten fingers. C comes from centum and M from mille, the Latin for one hundred and one thousand respectively. The Romans also used S for ‘a half’ and a system of fractions based on 12.

Roman number system

It’s not easy handling Roman numerals. For example, the meaning of MMMCDXLIIII only becomes transparent when brackets are mentally introduced so that (MMM)(CD)(XL)(IIII) is then read as 3000 + 400 + 40 + 4 = 3444. But try adding MMMCDXLIIII + CCCXCIIII. A Roman skilled in the art would have short cuts and tricks, but for us it’s difficult to obtain the right answer without first calculating it in the decimal system and translating the result back into Roman notation:

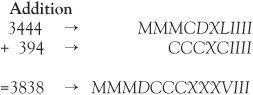
The multiplication of two numbers is much more difficult and might be impossible within the basic system, even to Romans! To multiply 3444 × 394 we need the medieval appendages.

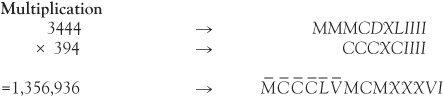
A Louis XIIII clock

The Romans had no specific symbol for zero. If you asked a vegetarian citizen of Rome to record how many bottles of wine he’d consumed that day, he might write III but if you asked him how many chickens he’d eaten, he couldn’t write 0. Vestiges of the Roman system survive in the pagination of some books (though not this one) and on the foundation stones of buildings. Some constructions were never used by the Romans, like MCM for 1900, but were introduced for stylistic reasons in modern times. The Romans would have written MDCCCC. The fourteenth King Louis of France, now universally known as Louis XIV, actually preferred to be known as Louis XIIII and made it a rule that his clocks were to show 4 o’clock as IIII o’clock.

Decimal whole numbers

We naturally identify ‘numbers’ with decimal numbers. The decimal system is based on ten using the numerals 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. Actually it is based on ‘tens’ and ‘units’ but units can be absorbed into ‘base 10’. When we write down the number 394, we can explain its decimal meaning by saying it is composed of 3 hundreds, 9 tens and 4 units, and we could write

394 = 3 × 100 + 9 × 10 + 4 × 1

This can be written using ‘powers’ of 10 (also known as ‘exponentials’ or ‘indices’),

394 = 3 × 10² + 9 × 10¹ + 4 × 10⁰

where 10² = 10 × 10, 10¹ = 10 and we agree separately that 10⁰ = 1. In this expression we see more clearly the decimal basis for our everyday number system, a system which makes addition and multiplication fairly transparent.

The point of decimal

So far we have looked at representing whole numbers. Can the decimal system cope with parts of a number, like 572/1000?

This means

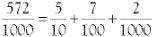
We can treat the ‘reciprocals’ of 10, 100, 1000 as negative powers of 10, so that

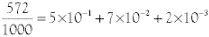
and this can be written .572 where the decimal point indicates the beginning of the negative powers of 10. If we add this to the decimal expression for 394 we get the decimal expansion for the number 394572/1000, which is simply 394.572.

For very big numbers the decimal notation can be very long, so we revert in this case to the ‘scientific notation’. For example, 1,356,936,892 can be written as 1.356936892 × 10⁹ which often appears as ‘1.356936892 × 10E9’ on calculators or computers. Here, the power 9 is one less than the number of digits in the number and the letter E stands for ‘exponential’. Sometimes we might want to use bigger numbers still, for instance if we were talking about the number of hydrogen atoms in the known universe. This has been estimated as about 1.7×10⁷⁷. Equally 1.7×10⁻⁷⁷, with a negative power, is a very small number and this too is easily handled using scientific notation. We couldn’t begin to think of these numbers with the Roman symbols.

Zeros and ones

While base 10 is common currency in everyday life, some applications require other bases. The binary system which uses base 2 lies behind the power of the modern computer. The beauty of binary is that any number can be expressed using only the symbols 0 and 1. The tradeoff for this economy is that the number expressions can be very long.

How can we express 394 in binary notation? This time we are dealing with powers of 2 and after some working out we can give the full expression as,

394 =1×256+1×128+0×64+0×32+0×16+1×8+0×4+1×2+0×1

so that reading off the zeros and ones, 394 in binary is 110001010 .

As binary expressions can be very long, other bases frequently arise in computing. These are the octal system (base 8) and the hexadecimal system (base 16). In the octal system we only need the symbols 0, 1, 2, 3, 4, 5, 6, 7, whereas hexadecimal uses 16 symbols. In this base 16 system, we customarily use 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. As 10 corresponds to the letter A, the number 394 is represented in hexadecimal as 18A. It’s as easy as ABC, which bear in mind, is really 2748 in decimal!

the condensed idea

Writing numbers down