When we try to solve simple algebraic equations using all these definitions, we soon discover some insoluble problems, such as the following. Suppose that we try to solve the equation b=3−5. That means, according to our definition of subtraction, that we must find a number which, when added to 5, gives 3. And of course, there is no such number, because we consider only positive integers; this is an insoluble problem. However, the plan, the great idea, is this: abstraction and generalization. From the whole structure of algebra, rules plus integers, we abstract the original definitions of addition and multiplication, but we leave the rules (22.1) and (22.2), and assume these to be true in general on a wider class of numbers, even though they are originally derived on a smaller class. Thus, rather than using integers symbolically to define the rules, we use the rules as the definition of the symbols, which then represent a more general kind of number. As an example, by working with the rules alone we can show that 3−5=0−2. In fact, we can show that one can make all subtractions, provided we define a whole set of new numbers: 0−1, 0−2, 0−3, 0−4, and so on, called the negative integers. Then we may use all the other rules, like a(b+c)=ab+ac and so forth, to find what the rules are for multiplying negative numbers, and we will discover, in fact, that all of the rules can be maintained with negative as well as positive integers.

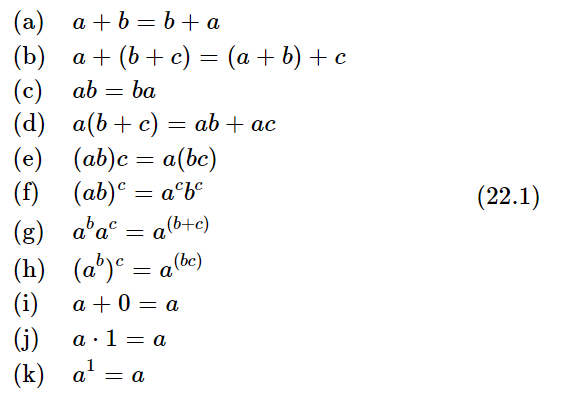
So, we have increased the range of objects over which the rules work, but the meaning of the symbols is different.

One cannot say, for instance, that −2 times 5 really means to add 5 together successively −2 times. That means nothing. But nevertheless, everything will work out all right according to the rules.

An interesting problem comes up in taking powers. Suppose that we wish to discover what a⁽³⁻⁵⁾ means. We know only that 3−5 is a solution of the problem, (3−5)+5=3. Knowing that, we know that a⁽³⁻⁵⁾a5=a³. Therefore a⁽³⁻⁵⁾=a³/a⁵, by the definition of division. With a little more work, this can be reduced to 1/a². So, we find that the negative powers are the reciprocals of the positive powers, but 1/a² is a meaningless symbol, because if a is a positive or negative integer, the square of it can be greater than 1, and we do not yet know what we mean by 1 divided by a number greater than 1!

Onward! The great plan is to continue the process of generalization; whenever we find another problem that we cannot solve we extend our realm of numbers. Consider division: we cannot find a number which is an integer, even a negative integer, which is equal to the result of dividing 3 by 5. But if we suppose that all fractional numbers also satisfy the rules, then we can talk about multiplying and adding fractions, and everything works as well as it did before.

Take another example of powers: what is a^3/5? We know only that (3/5)5=3, since that was the definition of 3/5. So we know also that (a^(3/5))⁵= a^(3/5)(5)= a³, because this is one of the rules. Then by the definition of roots we find that a^(3/5)=a^5√3.

In this way, then, we can define what we mean by putting fractions in the various symbols, by using the rules themselves to help us determine the definition—it is not arbitrary. It is a remarkable fact that all the rules still work for positive and negative integers, as well as for fractions!

We go on in the process of generalization. Are there any other equations we cannot solve? Yes, there are. For example, it is impossible to solve this equation: b= 2 ^1/2= √2. It is impossible to find a number which is rational (a fraction) whose square is equal to 2. It is very easy for us in modern days to answer this question. We know the decimal system, and so we have no difficulty in appreciating the meaning of an unending decimal as a type of approximation to the square root of 2. Historically, this idea presented great difficulty to the Greeks. To really define precisely what is meant here requires that we add some substance of continuity and ordering, and it is, in fact, quite the most difficult step in the processes of generalization just at this point. It was made, formally and rigorously, by Dedekind. However, without worrying about the mathematical rigor of the thing, it is quite easy to understand that what we mean is that we are going to find a whole sequence of approximate fractions, perfect fractions (because any decimal, when stopped somewhere, is of course rational), which just keeps on going, getting closer and closer to the desired result. That is good enough for what we wish to discuss, and it permits us to involve ourselves in irrational numbers, and to calculate things like the square root of 2 to any accuracy that we desire, with enough work.