Phase Space and Phase Density
المؤلف:
George W. Collins
المصدر:
The Fundamentals of Stellar Astrophysics
الجزء والصفحة:
p 25
3-5-2017
1443
Phase Space and Phase Density
Consider a volume of physical space that is small compared to the physical system in question, but still large enough to contain a statistically significant number of particles. The range of physical space in which this small volume is embedded may be infinite or finite as long as it is significantly larger than the small volume. First let a set of three Cartesian coordinates x1, x2, and x3 represent the spatial part of the volume. Then allow the additional three Cartesian coordinates v1, v2, and v3 represent the components of the velocity of the particles. Coordinates v1, v2, and v3 are orthogonal to the spatial coordinates. This simply indicates that the velocity and position are assumed to be uncorrelated. It also provides for a six-dimensional space which we call phase space. The volume of the space is
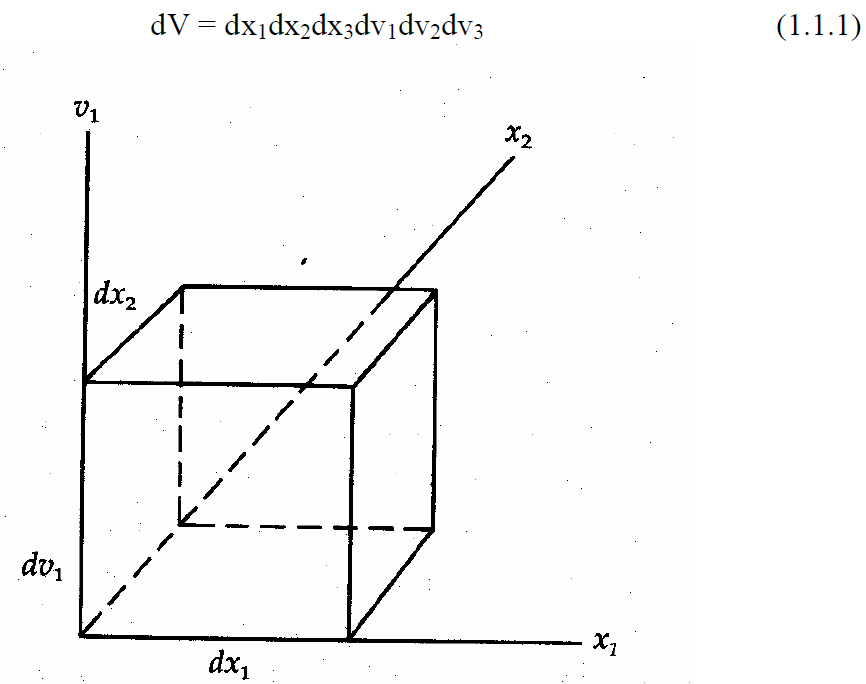
Figure 1.1 shows part of a small differential volume of phase space. It must be remembered that the position and velocity coordinates are orthogonal to each other.
If the number of particles in the small volume dV is N, then we can define a parameter f, known as the phase density, by
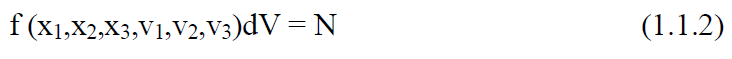
The manner in which a number of particles can be arranged in an ensemble of phase space volumes is described in Figure 1.1.
الاكثر قراءة في الفيزياء الرياضية
اخر الاخبار
اخبار العتبة العباسية المقدسة
