Integral
المؤلف:
Professor John W. Norbury
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
الجزء والصفحة:
p 246
1-1-2017
1513
Integral
1.1 Integral Equals Antiderivative
The derivative of y(x) = 3x is 
= 3. The derivative of y(x) = x2 is 
= 2x. The derivative of y(x) = 5x3 is = 15x2. Let's play a game. I tell you the answer and you tell me the question. Or I tell you the derivative and you tell me the original function y(x) that it came from. Ready?
We can generalize this to a rule.
Actually I have cheated. Let's look at the following functions
y(x) = 3x + 2
y(x) = 3x + 7
y(x) = 3x + 12
y(x) = 3x + C (C is an arbitrary constant)
y(x) = 3x
All of them have the same derivative = 3. Thus in our little game of re-constructing the original function y(x) from the derivative there is always an ambiguity in that y(x) could always have some constant added to it. Thus the correct answers in our game are
If = 3 then y(x) = 3x + constant
(Actually instead of always writing constant, let me just write C)
If = 2x then y(x) = x2 + C
If = 15x2 then y(x) = 5x3 + C
If = xn then 
This original function y(x) that we are trying to get is given a special name called the antiderivative or integral, but it's nothing more than the original function.
1.2 Integral Equals Area Under Curve
Let's see how to extract the integral from our original definition of derivative. The slope of a curve is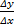 
or when the Δ increments are tiny. Notice that y(x) is a function of x but so also is . Let's call it
(1.1)
Thus if f(x) = = 2x then y(x) = x2 + C, and similarly for the other examples. In equation (1.1) I have written 
also because is just a tiny version of 
. Obviously then
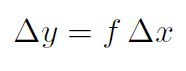(1.2)
or
(1.3)
What happens if I add up many Δy's. For instance suppose you are aged 18. Then if I add up many age increments in your life, such as
Age = ΔAge1 + ΔAge2 + ΔAge3 + ΔAge4….
1 year + 3 years + 0.5 year + 5 years + 0.5 year + 5 years + 3 years = 18 years
I get your complete age. Thus if I add up all possible increments of Δy I get back y. That is
or symbolically
(1.4)
where
(1.5)
Thus Δyi is an area of a little shaded region. Add them all up and we have the total area under the curve. Thus
(1.6)
Let's now make the little intervals Δyi and Δxi very tiny. Call them dy and dx. If I am using tiny intervals in my sum Σ I am going to use a new symbol ∫. Thus
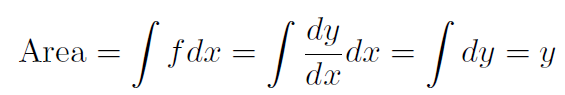(1.7)
which is just the tiny version of (1.6). Notice that the dx ''cancels".
In formula (1.7) recall the following. The derivative is 
and y is my original function which we called the integral or antiderivative. We now see that the integral or antiderivative or original function can be interpreted as the area under the derivative curve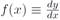 
. By the way ∫ f dx reads ''integral of f with respect to x."
Summary: if
Summary of 1.1 and 1.2
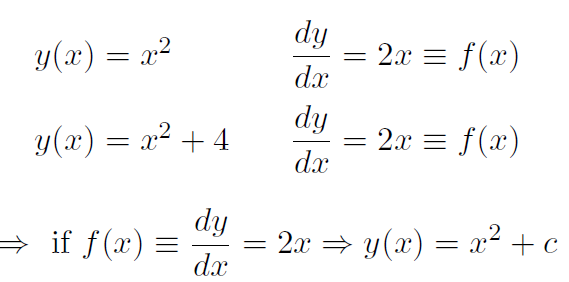
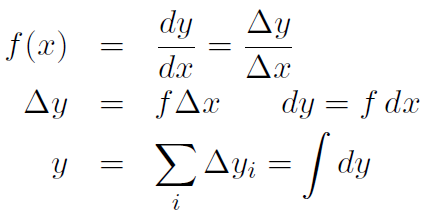
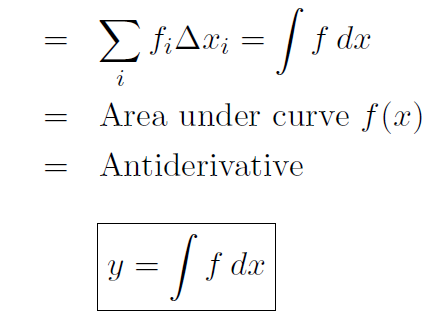
E.g.
do a few more examples.
Example What is ∫x dx?
Solution The derivative function is f(x) = = x. Therefore the original function must be 
. Thus
1.3 Definite and Indefinite Integrals
The integral ∫x dx is supposed to give us the area under the curve x, but our answer in the above example (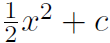
) doesn't look much like an area. We would expect the area to be a number.
Example What is the area under the curve f(x) = 4 between x1 = 1 and x2 = 6?
Solution This is easy because f(x) = 4 is just a horizontal straight line. The area is obviously 4 × 5 = 20.
Consider ∫ 4dx = 4x + c. This is called an indefinite integral or antiderivative. The integral which gives us the area is actually the definite integral written
(1.8)
Let's explain this. The formula 4x+c by itself does not give the area directly. For an area we must always specify x1 and x2 so that we know what area we are talking about. In the previous example we got 4 × 5 = 20 from 4x2 - 4x1 = (4 × 6) - (4 × 1) = 24 - 4 = 20, which is the same as (1.8). Thus (1.8) must be the correct formula for area. Notice here that it doesn't matter whether we include the c because it cancels out. Thus ∫ 4dx = 4x + c is the antiderivative or indefinite integral and it gives a general formula for the area but not the value of the area itself. To evaluate the value of the area we need to specify the edges x1 and x2 of the area under consideration as we did in (1.8). Using (1.8) to work out the previous example we would write
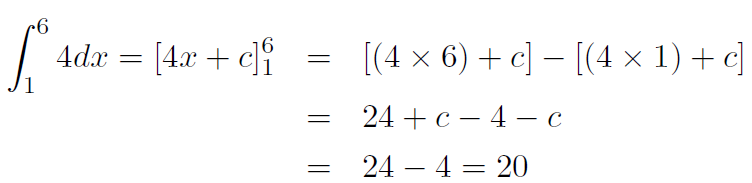(1.9)
Example Evaluate the area under the curve f(x) = 3x2 between x1 = 3 and x2 = 5.
Solution
الاكثر قراءة في الفيزياء الرياضية
اخر الاخبار
اخبار العتبة العباسية المقدسة
