James Joule

The Scientist as Amateur

James Joule’s story may seem a little hard to believe. He lived near Manchester, England in the scientific hinterland during much of Joule’s career where his family operated a brewery, making ale and porter. He did some of his most important work in the early morning and evening, before and after a day at the brewery. He had no university education, and hardly any formal training at all in science. As a scientist he was, in every way, an amateur. Like Mayer, who was also an amateur as a physicist, Joule was ignored at first by the scientific establishment. Yet, despite his amateur status, isolation, and neglect, he managed to probe more deeply than anyone else at the time (the early and middle 1840s) the tantalizing mysteries of conversion processes. And (unlike Mayer) he did not suffer prolonged neglect. The story of Joule’s rapid progress, from dilettante to a position of eminence in British science, can hardly be imagined in today’s world of research factories and prolonged scientific apprenticeships.

Equivalences

The theme that dominated Joule’s research from beginning to end, and served as his guiding theoretical inspiration, was the belief that quantitative equivalence could be found among thermal, chemical, electrical, and mechanical effects. He was convinced that the extent of any one of these effects could be assessed with the units of any one of the other effects. He studied such quantitative connections in no less than eight different ways: in investigations of chemical effects converted to thermal, electrical, and mechanical effects; of electrical effects converted to thermal, chemical, and mechanical effects; and of mechanical effects converted to thermal and electrical effects.

     At first, Joule did not fully appreciate the importance of mechanical effects in this scheme of equivalences. His earliest work centered on chemical, electrical, and thermal effects. In 1840, when he was twenty-two, he started a series of five investigations that was prompted by his interest in electrochemistry. (Joule was an electrochemist before he was a physicist.) First, he demonstrated accurately that the heating produced by an electrical current in a wire is proportional to the square of the current I and to the electrical resistance R the “I²R-heating law.” His experimental proof required temperature measurements in a “calorimeter” (a well-insulated, well-stirred vessel containing water or some other liquid), electrical current measurements with an instrument of his own design, and the invention of a system of absolute electrical units.

           Joule then invested considerable effort in various studies of the role played by his heating law in the chemical processes produced in electric cells. He worked with “voltaic cells,” which supply an electrical output (the modern flashlight battery is an example), and “electrolysis cells,” which consume an electrical input (for example, a cell that decomposes water into hydrogen gas and oxygen gas). In these experiments, Joule operated an electrolysis cell with a battery of voltaic cells. He eventually arrived at the idea that the electrical currents generated by the chemical reaction in the voltaic cell carried the reaction’s “calorific effect” or “chemical heat” away from the primary reaction site either to an external resistance where it could be converted to “free heat,” according to the I² R heating law, or to an electrolysis cell where it could be invested, all or partly, as “latent heat” in the electrolysis reaction.

      To determine the total chemical heat delivered to the electrolysis cell from the voltaic cells, call it Q_e, Joule found the resistance Re of a wire that could replace the electrolysis cell without causing other electrical changes, measured the current I in the wire, and calculated Q_e with the heating law as I²Re. He also measured the temperature rise in the electrolysis cell doubling as a calorimeter, and from it calculated the free heat Q_t generated in the cell. He always found that Q_e substantially exceeded Q_t; in extreme cases, there was no heating in the cell and Q_t was equal to zero. The difference Q_e - Q_t represented what Joule wanted to calculate: chemical heat converted to the latent heat of the electrolysis reaction. Representing the electrolysis reaction’s latent heat with Q_r, Joule’s calculation was

 Q_r = Q_e - Q_t .

         This is the statement Joule used in 1846 to determine several latent heats of electrolysis reactions with impressive accuracy. It is a complicated and exact application of the first law of thermodynamics, which Joule seems to have understood in terms of inputs and outputs to the electrolysis cell. That is evident in the last equation rearranged to

  Q_t = Q_e - Q_r,

with Q_e an input to the cell, Q_r an output because it is lost to the reaction, and Q_t the difference between the input and output (see fig. 1.1). This was a balancing or bookkeeping kind of calculation, and it implied a conservation assumption: the balanced entity could not be created or destroyed within the cell. Joule did not have a name for the conserved entity. It would be identified six years later by Rudolf Clausius and William Thomson, and called “energy” by Thomson. Although he had not arrived at the energy concept, Joule clearly did have, well

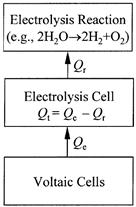
Figure 1.1. Input to and output from an electrolysis cell, according to Joule. The measured free heat Q_t in the cell depends only on the input Q_e from the voltaic cell and the output Q_r to the electrolysis reaction. It is equal to the input Q_e minus the output Q_r, that is, Q_t = Q_e - Q_r.

ahead of his contemporaries, a working knowledge of the first law of thermodynamics.

         Joule’s electrochemistry papers aroused little interest when they were first published, neither rejection nor acceptance, just silence. One reason for the indifference must have been the extraordinary nature of Joule’s approach. The input-output calculation was difficult enough to comprehend at the time, but in addition to that, Joule used his measured heats of electrolysis reactions to calculate heats of combustion reactions (that is, reactions with oxygen gas). For example, he obtained an accurate heat for the hydrogen combustion reaction,

                                                                         2 H₂ + O₂ → 2 H₂O,

which is just the reverse of the water electrolysis reaction,

                                                                           2 H₂O → 2 H₂ + O₂,

and therefore, Joule assumed, its heat had the same magnitude as that of the electrolysis reaction.

         This was an exotic way to study a combustion reaction. Joule’s first biographer, Osborne Reynolds, remarks that “the views they [the electrochemistry papers and others of Joule’s early papers] contained were so much in advance of anything accepted at the time that no one had sufficient confidence in his own opinion or was sufficiently sure of apprehending the full significance of the discoveries on which these views were based, to venture an expression of acceptance or rejection.” We can imagine a contemporary reader puzzling over the papers and finally deciding that the author was either a genius or a crank.

       But for Joule apparently unconcerned about the accessibility or inaccessibility of his papers for readers the complicated method was natural. His primary interest at the time was the accurate determination of equivalences among thermal, electrical, and chemical effects. He could imagine no better way to tackle this problem than to use electrical and calorimetric measurements to calculate the thermal effect of a chemical effect.

Mechanical Equivalents

Joule made the crucial addition of mechanical effects to his system of equivalences by following a time-honored route to scientific discovery: he made a fortunate mistake. In the fourth of his electrochemistry papers he reported electric potential data (voltages, in modern units) measured on voltaic cells whose electrode reactions produced oxidation of zinc and other metals. He believed, mistakenly, that these reaction potentials could be used in much the same way as reaction heats: that for a given reaction the potential had the same value no matter how the reaction was carried out. This interpretation is not sanctioned by modern thermodynamics unless cell potentials are measured carefully (reversibly). Joule and his contemporaries were unaware of this limitation, however, and the mistake led Joule to calculate electrical and thermal equivalents for the process in which dissolved oxygen is given “its elastic condition,” the reaction

                                                                 O₂ (solution) → O₂ (gas).

Joule’s result was an order of magnitude too large. But mistaken as it was quantitatively, the calculation advanced Joule’s conceptual understanding immensely, because he believed he had obtained electrical and thermal equivalents for a mechanical effect, the evolution of oxygen gas from solution. In Joule’s fertile imagination, this was suggestive. In the fourth electrochemistry paper, he remarked that he had already thought of ways to measure mechanical equivalents. He hoped to confirm the conclusion that “the mechanical and heating powers of a current are proportional to each other.”

        In this serendipitous way, Joule began the determinations of the mechanical equivalent of heat for which he is best known today. The first experiments in this grand series were performed in 1843, when Joule was twenty-four. In these initial experiments, he induced an electrical current in a coil of wire by rotating it mechanically in a strong magnetic field. The coil was contained in a glass tube filled with water and surrounded by insulation, so any heating in the coil could be measured by inserting a thermometer in the tube before and after rotating it in the magnetic field. The induced current in the coil was measured by connecting the coil to an external circuit containing a galvanometer. Although its origin was entirely different, the induced current behaved the same way as the voltaic current Joule had studied earlier: in both cases the current caused heating that followed the I ²R-law.

       In the final experiments of this design, the wheel of the induction device was driven by falling weights for which the mechanical effect, measured as a mechanical work calculation, could be made directly in foot-pounds (abbreviated ft-lb): one unit was equivalent to the work required to raise one pound one foot. Heat was measured by a unit that fit the temperature measurements: one unit raised the temperature of one pound of water 1^o Fahrenheit (F). We will use the term later attached to this unit, “British thermal unit,” or Btu.

       In one experiment, Joule dropped weights amounting to 4 lb 12 oz (= 4.75 lb) 517 feet (the weights were raised and dropped many times), causing a temperature rise of 2.46^o F. He converted the weight of the glass tube, wire coil, and water in which the temperature rise occurred all into a thermally equivalent weight of water, 1.114 lb. Thus the heating effect was 2.46^o F in 1.114 lb of water. If this same amount of heat had been generated in 1 lb of water, the heating effect would have been (2.46)(1.114)/1 = 2.74^o F. Joule concluded that in this case (517)(4.75) ft-lb was equivalent to 2.74 Btu. He usually determined the mechanical work equivalent to 1 Btu. That number, which Thomson later labeled J to honor Joule, was

for this experiment. This was one determination of the mechanical equivalent of heat. Joule did thirteen experiments of this kind and obtained results ranging from J = 587 to 1040 ft-lb per Btu, for which he reported an average value of 838 ft-lb per Btu. The modern “correct” value, it should be noted, is J = 778 ft-lb per Btu.

      If the ±27% precision achieved by Joule in these experiments does not seem impressive, one can sympathize with Joule’s critics, who could not believe his claims concerning the mechanical equivalent of heat. But the measurements Joule was attempting set new standards for experimental difficulty. According to Reynolds, the 1843 paper reported experiments that were more demanding than any previously attempted by a physicist.

        In any case, Joule was soon able to do much better. In 1845, he reported another, much different determination of the mechanical equivalent of heat, which agreed surprisingly well with his earlier measurement. In this second series of experiments, he measured temperature changes, and calculated the heat produced, when air was compressed. From the known physical behavior of gases he could calculate the corresponding mechanical effect as work done on the air during the compression.

     In one experiment involving compression of air, Joule calculated the work at 11230 ft-lb and a heating effect of 13.628 Btu from a measured temperature rise of 0.344^oF. The corresponding mechanical equivalent of heat was

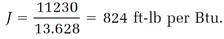
Another experiment done the same way, in which Joule measured the temperature change 0.128^oF, gave the result J = 796 ft-lb per Btu. Joule’s average for the two experiments was 810 ft-lb per Btu. This was in impressive, if somewhat fortuitous, agreement with the result J = 838 ft-lb per Btu reported in 1843.

       Joule also allowed compressed air to expand and do work against atmospheric pressure. Temperature measurements were again made, this time with a temperature decrease being measured. In one of these expansion experiments, Joule measured the temperature change -0.1738^oF and reduced this to 4.085 Btu. The corresponding work calculation gave 3357 ft-lb, so

Joule did two more experiments of this kind and measured the temperature changes -0.081^oF and -0.0855^oF, giving J = 814 and J = 760 ft-lb per Btu.

       When Joule’s colleagues looked at these results, the first thing they noticed was the accuracy claimed for measurements of very small temperature changes. In Joule’s time, accurate measurement of one-degree temperature changes was difficult enough. Joule reported temperature changes of tenths of a degree with three or four significant digits, and based his conclusions on such tiny changes. As William Thomson remarked, “Joule had nothing but hundredths of a degree to prove his case by.” Yet, most of Joule’s claims were justified. He made temperature measurements with mercury thermometers of unprecedented sensitivity and accuracy. He told the story of the thermometers in an autobiographical note: “It was needful in these experiments to use thermometers of greater exactness and delicacy than any that could be purchased at that time. I therefore determined to get some calibrated on purpose after the manner they had been by Regnault. In this I was ably seconded by Mr. Dancer [J. B. Dancer, a well-known Manchester instrument maker], at whose workshop I attended every morning for some time until we completed the first accurate thermometers which were ever made in England.”

        Joule demonstrated the heat-mechanical-work equivalence with a third gas expansion experiment that incorporated one of his most ingenious experimental designs. In this experiment, two constant-volume copper vessels, one evacuated and the other pressurized with air, were connected with a valve. The connected vessels were placed in a calorimeter, the valve opened, and the usual temperature measurements made. In this case, Joule could detect no net temperature change. Air expanding from the pressurized vessel was cooled slightly, and air flowing into the evacuated vessel was slightly heated, but no net temperature change was observed.

       This was what Joule expected. Because the combined system consisting of the two connected vessels was closed and had a fixed volume, all of the work was done internally, in tandem between the two vessels. Work done by the gas in one vessel was balanced by work done on the gas in the other; no net work was done. Heat equivalent to zero work was also zero, so Joule’s concept of heat mechanical- work equivalence demanded that the experiment produce no net thermal effect, as he observed.

        The next stage in Joule’s relentless pursuit of an accurate value for the mechanical equivalent of heat, which he had begun in 1847, was several series of experiments in which he measured heat generated by various frictional processes. The frictional effects were produced in a water-, mercury-, or oil-filled calorimeter by stirring with a paddle-wheel device, the latter being driven by falling weights, as in the 1843 experiments. The work done by the weights was converted directly by the paddle-wheel stirrer into heat, which could be measured on a thermometer in the calorimeter.

       Of all Joule’s inventions, this experimental design, which has become the best known monument to his genius, made the simplest and most direct demonstration of the heat-mechanical-work equivalence. This was the Joule technique reduced to its essentials. No complicated induction apparatus was needed, no calculational approximations, just falling weights and one of Joule’s amazingly accurate thermometers.

          With the paddle-wheel device and water as the calorimeter liquid, Joule obtained J = 773.64 ft-lb per Btu from a temperature rise of 0.563^oF. Using mercury in the calorimeter, he obtained J = 773.762 and 776.303 ft-lb per Btu. In two further series of experiments, Joule arranged his apparatus so the falling weights caused two cast-iron rings to rub against each other in a mercury-filled calorimeter; the results     J = 776.997 and 774.880 ft-lb per Btu were obtained.

      Joule described his paddle-wheel experiments in 1847 at an Oxford meeting of the British Association for the Advancement of Science. Because his previous papers had aroused little interest, he was asked to make his presentation as brief as possible. “This I endeavored to do,” Joule recalled later, “and a discussion not being invited the communication would have passed without comment if a young man had not risen in the section, and by his intelligent observations created a lively interest in the new theory.”

        The silence was finally broken. The young man was William Thomson, recently installed as professor of natural philosophy at Glasgow University. Thomson had reservations about Joule’s work, but he also recognized that it could not be ignored. “Joule is, I am sure, wrong in many of his ideas,” Thomson wrote to his father, “but he seems to have discovered some facts of extreme importance, as for instance, that heat is developed by the friction of fluids.” Thomson recalled in 1882 that “Joule’s paper at the Oxford meeting made a great sensation. Faraday was there, and was much struck by it, but did not enter fully into the new views. . . . It was not long after when Stokes told me he was inclined to be a Joulite.” George Stokes was another rising young physicist and mathematician, in 1847 a fellow at Pembroke College, Cambridge, and in two years to be appointed Lucasian Professor of Mathematics, the chair once occupied by Newton.

        During the three years following the Oxford meeting, Joule rose from obscurity to a prominent position in the British scientific establishment. Recognition came first from Europe: a major French journal, Comptes Rendu, published a short account of the paddle-wheel experiments in 1847, and in 1848 Joule was elected a corresponding member of the Royal Academy of Sciences at Turin. Only two other British scientists, Faraday and William Herschel, had been honored by the Turin Academy. In 1850, when he was thirty-one, Joule received the badge of British scientific acceptance: election as a fellow of the Royal Society.

         After these eventful years, Joule’s main research effort was a lengthy collaboration with Thomson, focusing on the behavior of expanding gases. This was one of the first collaborative efforts in history in which the talents of a theorist and those of an experimentalist were successfully and happily united.

Living Force and Heat

Joule believed that water at the bottom of a waterfall should be slightly warmer than water at the top, and he made attempts to detect such effects (even on his honeymoon in Switzerland, according to an apocryphal, or at any rate embellished, story told by Thomson). For Joule this was an example of the conservation principle that “heat, living force, and attraction through space . . . are mutually convertible into one another. In these conversions nothing is ever lost.” This statement is almost an expression of the conservation of mechanical and thermal energy, but it requires some translation and elaboration.

      Newtonian mechanics implies that mechanical energy has a “potential” and a “kinetic” aspect, which are linked in a fundamental way. “Potential energy” is evident in a weight held above the ground. The weight has energy because work was required to raise it, and the work can be completely recovered by letting the weight fall very slowly and drive machinery that has no frictional losses. As one might expect, the weight’s potential energy is proportional to its mass and to its height above the ground: if it starts at a height of 100 feet it can do twice as much work as it can if it starts at 50 feet.

       If one lets the weight fall freely, so that it is no longer tied to machinery, it does no work, but it accelerates and acquires “kinetic energy” from its increasing speed. Kinetic energy, like potential energy, can be converted to work with the right kind of machinery, and it is also proportional to the mass of the weight. Its relationship to speed, however, as dictated by Newton’s second law of motion, is to the square of the speed.

         In free fall, the weight has a mechanical energy equal to the sum of the kinetic and potential energies,

    mechanical energy = kinetic energy + potential energy.      (1)

As it approaches the ground the freely falling weight loses potential energy, and at the same time, as it accelerates, it gains kinetic energy. Newton’s second law informs us that the two changes are exactly compensating, and that the total mechanical energy is conserved, if we define

           (2)

   potential energy = mgz.      (3)

In equations (2) and (3), m is the mass of the weight, v its speed, z its distance above the ground, and g the constant identified above as the gravitational acceleration. If we represent the total mechanical energy as E, equation (1) becomes

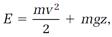          (4)

and the conservation law justified by Newton’s second law guarantees that E is always constant. This is a conversion process, of potential energy to kinetic energy, as illustrated in figure 1.2. In the figure, before the weight starts falling it has 10 units of potential energy and no kinetic energy. When it has fallen halfway to the ground, it has 5 units of both potential and kinetic energy, and in the instant before it hits the ground it has no potential energy and 10 units of kinetic energy. At all times its total mechanical energy is 10 units.

     Joule’s term “living force” (or vis viva in Latin) denotes mv², almost the same

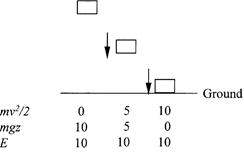
Figure 1.2. Illustration of the conversion of potential energy to kinetic energy by a freely falling weight, and the conservation of total mechanical energy.

thing as the kinetic energy mv²/2, and his phrase “attraction through space” means the same thing as potential energy. So Joule’s assertions that living force and attraction through space are interconvertible and that nothing is lost in the conversion are comparable to the Newtonian conservation of mechanical energy. Water at the top of the falls has potential energy only, and just before it lands in a pool at the bottom of the falls, it has kinetic energy only. An instant later the water is sitting quietly in the pool, and according to Joule’s principle, with the third conserved quantity, heat, included, the water is warmer because its mechanical energy has been converted to heat. Joule never succeeded in confirming this waterfall effect. The largest waterfall is not expected to produce a temperature change of more than a tenth of a degree. Not even Joule could detect that on the side of a mountain.

         Joule’s mechanical view of heat led him to believe further that in the conversion of the motion of an object to heat, the motion is not really lost because heat is itself the result of motion. He saw heat as the internal, random motion of the constituent particles of matter. This general idea had a long history, going back at least to Robert Boyle and Daniel Bernoulli in the seventeenth century.

         Joule pictured the particles of matter as atoms surrounded by rapidly rotating “atmospheres of electricity.” The centrifugal force of the atmospheres caused a gas to expand when its pressure was decreased or its temperature increased. Mechanical energy converted to heat became rotational motion of the atomic atmospheres. These speculations of Joule’s mark the beginning of the development of what would later be called the “molecular (or kinetic) theory of gases.” Following Joule, definitive work in this field was done by Clausius, Maxwell, and Boltzmann.

A Joule Sketch

Osborne Reynolds, who met Joule in 1869, gives us this impression of his manner and appearance in middle age: “That Joule, who was 51 years of age, was rather under medium height; that he was somewhat stout and rounded in figure; that his dress, though neat, was commonplace in the extreme, and that his attitude and movements were possessed of no natural grace, while his manner was somewhat nervous, and he possessed no great facility of speech, altogether conveyed an impression of simplicity, and utter absence of all affectation which had characterized his life.”

       Joule married Amelia Grimes in 1847, when he was twenty-nine and she thirty-three; they had two children, a son and a daughter. Amelia died in 1854 and “the shock took a long time to wear off,” writes Joule’s most recent biographer, Donald Cardwell. “His friends and contemporaries agreed that this never very assertive man became more withdrawn.” About fourteen years later, Joule fell in love again, this time with his cousin Frances Tappenden, known as “Fanny.” In a letter to Thomson he writes “an affection has sprung up between me and my cousin you saw when last here. There are hindrances in the way so that nothing may come of it.” The “hindrances” prevented marriage, and eventually Fanny married another man.

        Joule’s political leanings were conservative. He had a passionate, sometimes irrational, dislike of reform-minded Liberal politicians such as William Gladstone and John Bright. In a letter to John Tyndall, he wrote, “The fact is that Mr. Gladstone was fashioning a neat machine of ‘representation’ with the object of keeping himself in power. . . . Posterity will judge him as the worst ‘statesman’ that England ever had and the verdict with regard to that Parliament will be ditto, ditto.”

      Joule had a personality that was “finely poised,” as another biographer, J. G. Crowther, puts it. On the one hand he was conducting experiments with unlimited care and patience, and on the other hand fulminating against Liberal politicians. He feared that too much mental effort would threaten his health. In 1860, a new professorship of physics was created at Owens College in Manchester, and

      Joule could have had it, but he decided not to apply, as he explained in a letter to Thomson: “I have not the courage to apply for the Owens professorship. The fact is that I do not feel it would do for me to overtask my brain. A few years ago, I felt a very small mental effort too much for me, and in consequence spared myself from thought as much as possible. I have felt a gradual improvement, but I do not think it would be well for me to build too much on it. I shall do a great deal more in the long run by taking things easily.”

      Joule’s life was hectic and burdensome at this time, and he may have felt that he was near breakdown. Amelia died in 1854, the brewery was sold in the same year, and the experiments with Thomson were in progress. During the next six years, he moved his household and laboratory twice. After the second move, he was upset by an acrimonious dispute with a neighbor who objected to the noise and smoke made by a three-horsepower steam engine Joule included in his apparatus. The neighbor was “a Mr Bowker, an Alderman of Manchester and chairman of the nuisances committee, a very important man in his own estimation like most people who have risen from the dregs of society.”

       During this same period, Joule narrowly escaped serious injury in a train wreck, and after that he had an almost uncontrollable fear of railway travel. At the same time, he loved to travel by sea, even when it was dangerous. In a letter to Fanny, he described a ten-mile trip to Tory Island, in the Atlantic off the coast of Ireland, where his brother owned property: “Waves of 4 to 600 feet from crest to crest and 20 feet high. Dr Brady who was with us and had yachted in the ocean for 25 years said he was never in a more dangerous sea. However the magnificence of it took away the disagreeable sense of danger which might have prevailed.”

     In some measures of scientific ability, Joule was unimpressive. As a theorist, he was competent but not outstanding. He was not an eloquent speaker, and he was not particularly important in the scientific establishment of his time. But Joule had three things in extraordinary measure experimental skill, independence, and inspiration.

         He was the first to understand that unambiguous equivalence principles could be obtained only with the most inspired attention to experimental accuracy. He accomplished his aim by carefully selecting the measurements that would make his case. Crowther marvels at the directness and simplicity of Joule’s experimental strategies: “He did not separate a quantity of truth from a large number of groping unsuccessful experiments. Nearly all of his experiments seem to have been perfectly conceived and executed, and the first draft of them could be sent almost without revision to the journals for publication.”

     For most of his life, Joule had an ample independent income. That made it possible for him to pursue a scientific career privately, and to build the kind of intellectual independence he needed. Crowther tells us about this facet of Joule’s background:

           As a rich young man he needed no conventional training to qualify him for a career, or introduce him to powerful future friends. His early researches were pursued partly in the spirit of a young gentleman’s entertainment, which happened to be science instead of fighting or politics or gambling. It is difficult to believe that any student who had received a lengthy academic training could have described researches in Joule’s tone of intellectual equality. The gifted student who has studied under a great teacher would almost certainly adopt a less independent tone in his first papers, because he would have the attitude of a pupil to his senior, besides a deference due to appreciation of his senior’s achievements. A student without deference after distinguished tuition is almost always mediocre.

        Joule was not entirely without distinguished tuition. Beginning in 1834, and continuing for three years, Joule and his brother Benjamin studied with John Dalton, then sixty-eight and, as always, earning money teaching children the rudiments of science and mathematics. The Joules’ studies with Dalton were not particularly successful pedagogically. Dalton took them through arithmetic and geometry (Euclid) and then proceeded to higher mathematics, with little attention to physics and chemistry. Dalton’s syllabus did not suit Joule, but he benefited in more-informal ways. Joule wrote later in his autobiographical note, “Dalton possessed a rare power of engaging the affection of his pupils for scientific truth; and it was from his instruction that I first formed a desire to increase my knowledge by original researches.” In his writings, if not in his tutoring, Dalton emphasized the ultimate importance of accurate measurements in building the foundations of physical science, a lesson that Joule learned and used above all others. The example of Dalton, internationally famous for his theories of chemical action, yet self-taught, and living and practicing in Manchester, must have convinced Joule that he, too, had prospects.

       Joule’s independence and confidence in his background and talents, natural or learned from Dalton, were tested many times in later years, but never shaken. His first determination, in 1843, of the mechanical equivalent of heat was ignored, and subsequent determinations were given little attention until Thomson and Stokes took notice at the British Association meeting in 1847.

       When Joule submitted a summary of his friction experiments for publication, he closed the paper with three conclusions that asserted the heat-mechanical work equivalence in the friction experiments, quoted his measured value of J, and stated that “the friction consisted in the conversion of mechanical power to heat.” The referee who reported on the paper (believed to have been Faraday) requested that the third conclusion be suppressed.

       Joule’s first electrochemistry paper was rejected for publication by the Royal Society, except as an abstract. Arthur Schuster reported that, when he asked Joule what his reaction was when this important paper was rejected, Joule’s reply was characteristic: “I was not surprised. I could imagine those gentlemen sitting around a table in London and saying to each other: ‘What good can come out of a town [Manchester] where they dine in the middle of the day?’ ”

      But with all his talents, material advantages, and intellectual independence, Joule could never have accomplished what he did if he had not been guided in his scientific work by inspiration of an unusual kind. For Joule “the study of nature and her laws” was “essentially a holy undertaking.” He could summon the monumental patience required to assess minute errors in a prolonged series of measurements, and at the same time transcend the details and see his work as a quest “for acquaintance with natural laws . . . no less than an acquaintance with the mind of God therein expressed.” Great theorists have sometimes had thoughts of this kind one might get the same meaning from Albert Einstein’s remark that “the eternal mystery of the world is its comprehensibility” but experimentalists, whose lives are taken up with the apparently mundane tasks of reading instruments and designing apparatuses, have rarely felt that they were communicating with the “mind of God.”

        It would be difficult to find a scientific legacy as simple as Joule’s, and at the same time as profoundly important in the history of science. One can summarize Joule’s major achievement with the single statement

    J = 778 ft-lb per Btu,

and add that this result was obtained with extraordinary accuracy and precision. This is Joule’s monument in the scientific literature, now quoted as 4.1840 kilogram-meters per calorie, used routinely and unappreciatively by modern students to make the quantitative passage from one energy unit to another.

           In the 1840s, Joule’s measurements were far more fascinating, or disturbing, depending on the point of view. The energy concept had not yet been developed (and would not be for another five or ten years), and Joule’s number had not found its niche as the hallmark of energy conversion and conservation. Yet Joule’s research made it clear that something was converted and conserved, and provided vital clues about what the something was.