لتفهم السبب في أن خطوط حيود الأشعة السينية من المساحيق تصبح ذات عرض أكبر من الطبيعي في حالة البلورات صغيرة الحجم سنعيد التفكير في استنباط قانون براج على أن نمتد بالطريقة لتشمل عملية التقوية غير الكاملة للموجات المشتتة بواسطة مستويات الشبيكة المتتالية، فقانون براج (λ = θ 2d sin) يتم اشتقاقه بأن نجد الظروف التي تكون فيها الموجات المنعكسة من كل المستويات في البلورة متحدة في الطور مع بعضها البعض. وعلى أي حال سيكون هناك كمية محسوسة من الأشعة مشتتة حتى لو كان القانون غير متحقق تماما (بدقة).

وفيما يلي سنوضح أن الانحراف الممكن حدوثه عن تحقيق هذا القانون سيكون أكبر إذا كانت البلورات أصغر. ففي حالة البلورات الصغيرة يكون الانحراف (البعد) كبير لدرجة كبيرة حتى أن الانعكاسات تبدو واضحة على مدى أوسع من الزوايا وبذلك تسمى الخطوط: خطوطا عريضة.

القيمة العددية للعرض يمكن استنتاجها بطريقة بسيطة وضعها A. R. Stokes ستوكس.

نفترض شعاعا من الأشعة السينية يسقط على مجموعة من المستويات 2m بزاوية dθ + θ حيث يتشتت بنفس الزاوية (يتضح من الشكل أنه إذا لم يتحقق ذلك الشرط فإنه لن يحدث أي شعاع ضعيف متشتت من المستويات الممتدة). δθ هي زاوية الانحراف (البعد) عن زاوية براج θ لانعكاس من مستويات الشبيكة.

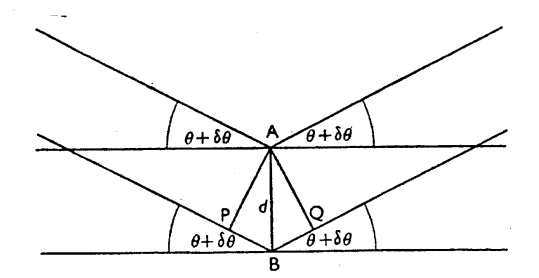
شكل (2-11)

اشعة سينية ساقطة على مستويات شبيكة بلورية بزاوية تختلف قليلا عن زاوية براج

يتضح من الشكل (2-11) أن الفرق في المسار PBQ للموجات المشتتة من المستويات المتعاقبة هو (δθ + θ) 2d sin وشرط التقوية الكاملة للموجات هو بالطبع

θ2d sin  = λ. ولكن نفترض أن δθ لها قيمة بحيث إن المستوى 1 + m يقوم بتشتيت الموجات بحيث يكون الفرق في الطور بين هذه الموجات والتي تتشتت من المستوى الأول يساوي 180º أي أن:

فإذا كانت المعادلة (8-11) صحيحة للمستوى الأول والمستوى 1+m فإنها ستكون صحيحة أيضا لأي مستويين لهما نفس الإزاحة (المسافة الفاصلة Separation) وذلك حتى المستويات 2m، m.

وعلى ذلك فإن البلورة يمكن تقسيمها لجزئين حيث يكون التشتت من الجزء الأول منها له فرق في الطور يساوي 180º عن ذلك المتشتت من الجزء الثاني وبذلك يلاشى كل منهما الآخر. وقيمة الزاوية δθ المبين بالمعادلة (8-11)،(9-11) تكون هي القيمة المقابلة لتشتت قيمته الصفر.

وقيمة الزاوية δθ يمكن استنتاجها بطرح المعادلة (9-11) المعادلة (8-11)  الذي يعطي ...

حيث 2 md = t هي سمك البلورة والتشتت من البلورة يكون أيضا مساويا للصفر عندما تكون

δθ = λ /2t cos θ

وبذلك تكون الزاوية بين الاتجاهين اللذين يكون عندهما التشتت مساويا للصفر هي θ λ/t cos. وهذه القيمة لا يمكن اعتبارها قيمة دقيقة في ظل الافتراض الذي وضع عند اشتقاقها.

وباستخدام مفهوم الشبيكة المقلوبة نعبر عن العرض الزائد للانعكاسات بأنه زيادة في مساحة النقطة في الشبيكة المقلوبة، فإذا كانت البلورة كروية الشكل ولها نصف قطر t تكون كل نقطة في الشبيكة المقلوبة لها نصف قطر

δθ = λ /t cos θ

وفي هذه الحالة تكون المسافة من مركز الشبيكة في الفراغ المقلوب مساوية للكمية.

λ/d = 2 sin θ                                     (11-11)

وبذلك يكون قطر كل نقطة في الشبيكة المقلوبة 2 sin θ)) δ مساويا للكمية θ δ θ cos 2.

ومن قيمة δθ الموضحة فيما سبق نجد أن قطر كل نقطة في الشبيكة المقلوبة يعطى بالمعادلة ...

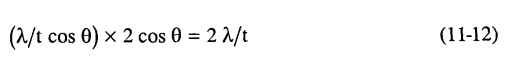
وهي قيمة لا تعتمد على θ، وعلى هذا فكل نقط الشبيكة المقلوبة تكون ذات عرض واحد (شكل 3-11).

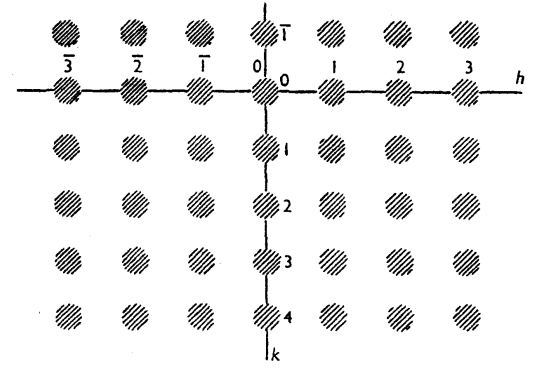
شكل (3-11)

مقطع في الشبيكة المقلوبة لبلورة كروية صغيرة الحجم