Set covering deployment (sometimes written "set-covering deployment" and abbreviated SCDP for "set covering deployment problem") seeks an optimal stationing of troops in a set of regions so that a relatively small number of troop units can control a large geographic region. ReVelle and Rosing (2000) first described this in a study of Emperor Constantine the Great's mobile field army placements to secure the Roman Empire. Set covering deployment can be mathematically formulated as a (0,1)-integer programming problem.

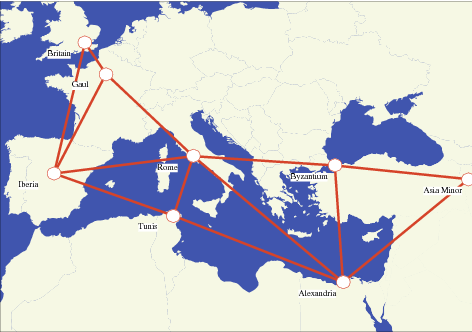
To formulate the Roman domination problem, consider the eight provinces of the Constantinian Roman Empire illustrated above. Each region is represented as a white disk, and the red lines indicate region connections. Call a region secured if one or more field armies are stationed in that region, and call a region securable if a field army can be deployed to that area from an adjacent area. In addition, assume that a field army can only be deployed to an adjacent region if at least one army remains in the original region to provide logistical support. Also assume that each region contains at most two armies, as the number of available armies are limited and cannot be concentrated in any one region.

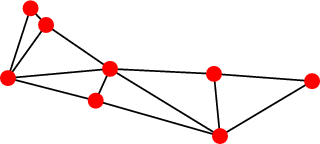
This problem can then be mathematically formulated by representing the Empire as a graph 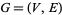 with vertex set  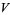and edge set 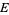. We can then associate two binary variables  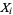and 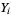 with each vertex 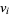(i.e., each province) in the vertex set  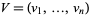of the Roman Empire graph which specify whether a first and second field army (respectively) is located at a given vertex 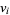. In the terminology of graph theory, the Roman Empire graph is a simple connected graph on eight vertices and with 13 edges.

In set covering deployment, the problem to be solved is to maximize the quantity 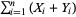 subject to the constraints

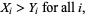(1)

which guarantees that the first legion is stationed at a given vertex before a second can be,

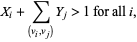(2)

which guarantees that if 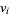 does not contain a field army, it has a neighbor with two field armies, and

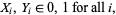(3)

which enforces the integer constraint (i.e., when combined with the first constraint, only zero, one, or two field armies may be placed in any given region). This integer programming problem can then be translated into matrix terms and solved using standard techniques to find the minimum number of field armies needed to secure the Constantinian Roman Empire (ReVelle and Rosing 2000, Rubalcaba 2005).

In the Season 4 opening episode "Trust Metric" (2007) of the television crime drama NUMB3RS, math genius Charlie Eppes uses set covering deployment as an analogy for optimizing the position of police officers in downtown Los Angeles in a search for escaped fugitives.

REFERENCES:

ReVelle, C. S. and Rosing, K. E. "Defendens Imperium Romanum: A Classical Problem in Military Strategy." Amer. Math. Monthly 107, 585-594, 2000.

Rubalcaba, R. R. "Fractional Domination, Fractional Packings, and Fractional Isomorphisms of Graphs." Ph.D. dissertation. Auburn, Alabama: Auburn University. May 13, 2005. http://webpages.uah.edu/~rubalcr/RUBALCABA.pdf.

اخر الاخبار

اخبار العتبة العباسية المقدسة

جولة تفقدية لمتابعة خطة تنظيم مداخل المعزّين المشاركين في عزاء ركضة طويريج

لتعزيز التعاون الأكاديمي والبحثي.. جامعة الكفيل توقع اتفاقيتي توأمة مع جامعتين عراقيتين

المجمَع العلميّ يواصل إقامة مجلسه العزائي بذكرى شهادة الإمام الحسين (عليه السلام) في النجف الأشرف

قسم حفظ النظام يواصل تنفيذ خطته لتنظيم سير المواكب والزائرين في شهر المحرم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد