المفاهيم الأساسية للدوال الحقيقية

FUNDAMENTAL CONEPT OF REAL FUNCTIONS            

مفهوم الدالة : Definition of Function

هو علاقة بين مجموعتين (y , x) بحيث يرتبط كل عنصر من عناصر المجموعة الأولى (x) بعنصر واحد فقط من عناصر المجموعة الثانية (y).

ومفهوم الاقتران أو الدالة هو علاقة بين مجموعتين : الأولى تسمى المجال والثانية تسمى المجال المقابل. بحيث إن كل عنصر في المجال له صورة واحدة فقط في المجال المقابل. أما مدى الاقتران : فهو المجموعة الجزئية من المجال المقابل المكونة من جميع صور المجال. وإذا لم يحدد المجال فهو اكبر مجموعة جزئية من الأعداد الحقيقية التي يكون الاقتران معرفاً عليها. ونظراً لأهمية الدوال، فسوف نتعرض إلى المزيد من خصائصها، وطرق تمثيلها بيانياً .

المجال Domain : هو مجموعة قيم x "المجموعة الأولى".

المجال المقابل Co Domain : هو مجموعة قيم  y "المجموعة الثانية".

المدى Range : هو مجموعة قيم y التي لها أصل في x "المرتبطة بعناصر x".

ملاحظة مهمة : المجال المقابل للدالة نعتبره دائماً IR ما لم يذكر خلاف ذلك، وهو المجموعة الشاملة لعناصر المدى ، "أي أن المدى ⸧ المجال المقابل".

الدالة الحقيقية Real Function : هي التي كل من مجالها ومجالها المقابل مجموعة الأعداد الحقيقية (IR) او جزء منها.

تعريف الدالة : تسمى الاقتران f الذي يقرن ويربط بين عناصر المجموعة D ومجموعة المدى IR بأنه دالة (function) إذا تحقق ما يلي:

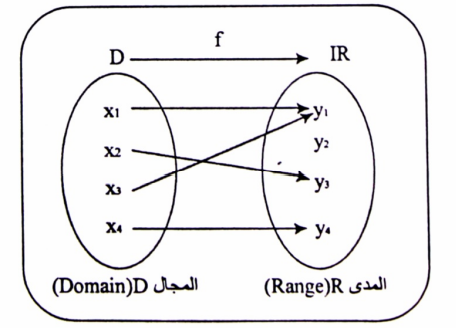
لكل عنصر x من مجموعة المجال (Domain) D له صورة واحدة فقط y في مجموعة المدى R (Range) . يسمى عنصر المجال (بالسابقة) ويسمى عنصر المدى (باللاحقة). ونكتب

بيانياً نقول عن بيان إنه لدالة إذا كان المستقيم المتعامد مع محور (y = b, y∊IR)، فإنه يقطع المنحني في نقطة واحدة، نقطة واحدة على الأكثر.

شكل (1-1)

إن البيان الممثل في الشكل (1-1) هو دالة، رغم وجود نقاط في المجموعة IR ليس لها سوابق ، ولاحقة لها اكثر من سابقة واحدة.

مثال (1) : إن البيان الممثل في الشكل (1-2) هو دائرة وليس منحني دالة، ونلاحظ أن لبعض قيم x أكثر من صورة، وهذا ما يتعارض مع تعريف الدالة.

شكل (1-2)

مثال (2) : إن البيان الممثل في الشكل (1-3) جزء قطع مكافئ ليس منحنى دالة، ونلاحظ أن لبعض قيم x أكثر من صورة، وهذا ما يتعارض مع تعريف الدالة.

شكل (1-3)

مثال (3) : إن البيان الممثل في الشكل  (1-4) للجزء الموجب من الدائرة هو منحنى دالة، لأن لكل قيم x صورة واحدة فقط، وهو تعريف الدالة.

شكل (1-4)

مثال (4) : إن البيان الممثل في الشكل (1-5) للجزء الموجب للقطع المكافئ على محور (OY) هو منحنى دالة، لأن لكل قيم x صورة واحدة فقط، وهو تعريف الدالة.

شكل (1-5)

ملاحظات :

1- الدالة هي امتداد للتطبيق (الاقتران)، وهي بنفس ذاتها لها تمديد يسمى بالقطوع المكافئة الذي يعبر عن اتحاد دالتين ، ثم بحد ذاتها يتم تمديدها إلى القياسات التي تتمدد إلى التوزيعات، ثم تتمدد إلى ما يسمى بالتغيرات. كل هذه الأشكال تسمح لنا بقدر من المرونة في التعبير عن الواقع بالنماذج الرياضية التي من خلالها نستطيع اكتشاف بعض خفايا الظواهر.

2- الدالة عندما يتم تعريفها على مجموعة لتعريف يتطابق مفهومها مع مفهوم الاقتران (التطبيق) . أي ان مفهوم الدالة أشمل من مفهوم التطبيق الذي هو اوسع من العلاقة.

أنواع الدوال : تصنف الدوال حسب طبيعتها الرياضية ومجال استخدامها، وقوتها الرياضية كالاشتقاق والتكامل، ونشير هنا إلى بعض الدوال الخاصة البسيطة ومنها .