

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Conway Game
المؤلف:
Berlekamp, E. R.; Conway, J. H.; and Guy, R. K
المصدر:
Winning Ways for Your Mathematical Plays. Wellesley, MA: A K Peters, 2004.
الجزء والصفحة:
...
19-10-2021
1750
Conway Game
Conway games were introduced by J. H. Conway in 1976 to provide a formal structure for analyzing games satisfying certain requirements:
1. There are two players, Left and Right (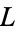 and
and 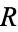 ), who move alternately.
), who move alternately.
2. The first player unable to move loses.
3. Both players have complete information about the state of the game.
4. There is no element of chance.
For example, nim is a Conway game, but chess is not (due to the possibility of draws and stalemate). Note that Conway's "game of life" is (somewhat confusingly) not a Conway game.
A Conway game is either:
1. The zero game, denoted as 0 or {|}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline3.gif" style="height:18px; width:19px" />, or
2. An object (an ordered pair) of the form {G^L|G^R}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline4.gif" style="height:21px; width:53px" />, where
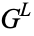 and
and 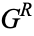 are sets of Conway games.
are sets of Conway games.
The elements of 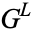 and
and 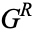 are called the Left and Right options respectively, and are the moves available to Left and Right. For example, in the game
are called the Left and Right options respectively, and are the moves available to Left and Right. For example, in the game {{a,b}|{}}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline9.gif" style="height:18px; width:61px" />, if it is
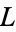 's move, he may move to
's move, he may move to 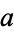 or
or 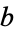 , whereas if it is
, whereas if it is 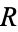 's move, he has no options and loses immediately.
's move, he has no options and loses immediately.
A game in which both players have the same moves in every position is called an impartial game. A game in which players have different options is a partisan game. A game with only finitely many positions is called a short game. A game in which it is possible to return to the starting position is called loopy.
Some simple games which occur frequently in the theory have abbreviated names:
1. {0|0}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline14.gif" style="height:18px; width:62px" />
2. {0|}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline15.gif" style="height:18px; width:47px" />
3. {n-1|}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline16.gif" style="height:18px; width:69px" /> for any positive integer
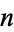
4. {0|1}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline18.gif" style="height:18px; width:72px" />
5. {0|*}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline19.gif" style="height:18px; width:63px" />
6. {*|0}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline20.gif" style="height:18px; width:65px" />
A recursive construction procedure can be used to generate all short games. Steps in the procedure are called days, and the set of games first appearing (born) on day 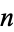 is denoted
is denoted 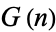 . The zeroth day is
. The zeroth day is {0}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline23.gif" style="height:15px; width:62px" />. Subsequent days are
{{L|R}}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline24.gif" style="height:18px; width:103px" /> where
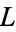 and
and 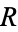 range over all elements of
range over all elements of 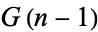 . Day 1 has four elements,
. Day 1 has four elements, {0,*,1,-1}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline28.gif" style="height:15px; width:121px" />, and the number of elements in
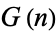 for
for 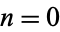 , 1, ... are 1, 4, 22, 1474, ... (OEIS A065401). D. Hickerson and R. Li found
, 1, ... are 1, 4, 22, 1474, ... (OEIS A065401). D. Hickerson and R. Li found 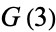 in 1974, but no other terms are known.
in 1974, but no other terms are known.
The following pairifaction table shows 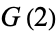 in terms of their left and right options:
in terms of their left and right options:
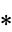 |
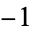 |
0 | 1 | ||
| 1 | 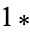 |
||||
| 0 | 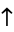 |
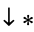 |
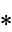 |
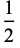 |
|
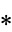 |
0 | 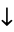 |
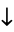 |
0 | |
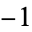 |
0 | 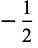 |
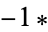 |
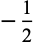 |
0 |
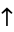 |
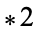 |
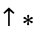 |
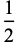 |
The set of all Conway games forms an Abelian group with the operations:
{(G^L+H) union (G+H^L)|(G^R+H) union (G+H^R)}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline60.gif" style="height:21px; width:317px" />
{-G^R|-G^L}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline61.gif" style="height:21px; width:110px" />
Here, expressions of the form 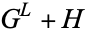 mean the set of all expressions of the form
mean the set of all expressions of the form 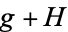 with
with 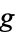 in
in 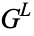 .
.
The set of all Conway games forms a partial order with respect to the comparison operations:
1. 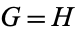 . If the second player to move in the game
. If the second player to move in the game 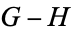 can win (
can win (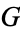 and
and 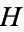 are equal).
are equal).
2. 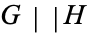 . If the first player to move in the game
. If the first player to move in the game 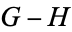 can win (
can win (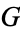 and
and 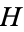 are fuzzy).
are fuzzy).
3. 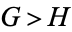 . If Left can win the game
. If Left can win the game 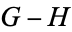 whether he plays first or not (
whether he plays first or not (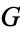 is greater than
is greater than 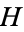 ).
).
4. 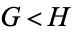 . If Right can win the game
. If Right can win the game 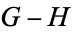 whether he plays first or not (
whether he plays first or not (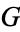 is less than
is less than 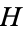 ).
).
We have denoted 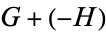 by
by 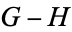 .
. 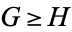 will mean either
will mean either 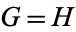 or
or 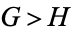 , and similarly for
, and similarly for 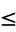 . For example, we have
. For example, we have 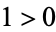 ,
, 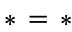 , and
, and 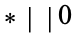 .
.
Each 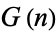 is a partial order with respect to the relation
is a partial order with respect to the relation 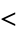 .
.
A basic theorem shows that all games may be put in a canonical form, which allows an easy test for equality. The canonical form depends on two types of simplification:
1. Removal of a dominated option: if {{L_1,L_2,...}|G^R}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline93.gif" style="height:21px; width:131px" /> and
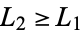 , then
, then {{L_2,...}|G^R}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline95.gif" style="height:21px; width:109px" />; and if
{G^L|{R_1,R_2,...}}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline96.gif" style="height:21px; width:133px" /> and
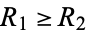 , then
, then {G^L|{R_2,...}}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline98.gif" style="height:21px; width:110px" />.
2. Replacement of reversible moves: if {{{A^L|{A^(R_1),A^(R_2),...}},G^(L_2),...}|G^R}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline99.gif" style="height:21px; width:245px" />, and
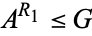 , then
, then {{{A^(R_1^L)},G^(L_2),...}|G^R}" src="https://mathworld.wolfram.com/images/equations/ConwayGame/Inline101.gif" style="height:27px; width:170px" />.
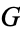 is said to be in canonical form if it has no dominated options or reversible moves. If
is said to be in canonical form if it has no dominated options or reversible moves. If 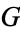 and
and 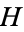 are both in canonical form, they both have the same sets of left and right options and so are equal.
are both in canonical form, they both have the same sets of left and right options and so are equal.
REFERENCES:
Berlekamp, E. R.; Conway, J. H.; and Guy, R. K. Winning Ways for Your Mathematical Plays. Wellesley, MA: A K Peters, 2004.
Calistrate, D.; Paulhus, M; and Wolfe, D. "On the Lattice Structure of Finite Games." In More Games of No Chance (Ed. R. J. Nowakowski). Cambridge, England: Cambridge University Press, pp. 25-30, 2002.
Conway, J. H. On Numbers and Games. Wellesley, MA: A K Peters, 2000.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 283-284, 1996.
Fraser, W.; Hirshberg, S.; and Wolfe, D. "The Structure of the Distributive Lattice of Games Born by Day 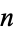 ." http://homepages.gac.edu/~wolfe/papers/dayn/structure.pdf.
." http://homepages.gac.edu/~wolfe/papers/dayn/structure.pdf.
Gonshor, H. An Introduction to Surreal Numbers. Cambridge, England: Cambridge University Press, 1986.
Knuth, D. Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness. Reading, MA: Addison-Wesley, 1974. http://www-cs-faculty.stanford.edu/~knuth/sn.html.
Schleicher, D. and Stoll, M. "An Introduction to Conway's Numbers and Games." http://arxiv.org/abs/math.CO/0410026.
Siegel, A. N. "Loopy Games and Computation." Ph.D. thesis. Berkeley, CA: University of California Berkeley, 2005.
Sloane, N. J. A. Sequence A065401 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















